
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
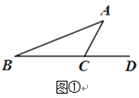
【题目】感知:如图①,∠ACD为△ABC的外角,易得∠ACD=∠A+∠B(不需证明) ;
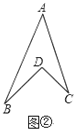
探究:如图②,在四边形ABDC中,试探究∠BDC与∠A、∠B.、∠C之间的关系,并说明理由;
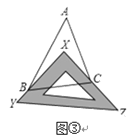
应用:如图③,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=_______度;(直接填答案,不需证明)
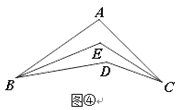
拓展:如图④,BE平分∠ABD,CE平分∠ACD,若∠BAC=100°,∠BDC=150°,则∠BEC=_______度. (直接填答案,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“五一劳动节”,某超市开展促销活动,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要108元,买3件A商品和4件B商品需要94元.问:打折后,若买5件A商品和4件B商品仅需86元,比打折前节省了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 ![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
A.(-3,0)
B.(-2,0)
C.x=-3
D.x=-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
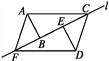
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1 , x2满足x1+x2=4和x1x2=3,那么二次函数ax2+bx+c(a>0)的图象有可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明题
(1)已知一元二次方程x2+px+q=0(p2-4q≥0)的两根为x1、x2;求证:x1+x2=-p , x1 x2=q .
(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com