
【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).

(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
【答案】(1)(18﹣2t);(2)t=6时,能使OP=OQ;(3)点P追上点Q需要18s,此时点Q已经停止运动.
【解析】
试题分析:(1)利用P点运动速度以及OM的距离进而得出答案;
(2)利用OP=OQ列出方程求出即可;
(3)利用假设追上时,求出所用时间,进而得出答案.
解:(1)∵P点运动速度为2cm/s,MO=18cm,
∴当点P在MO上运动时,PO=(18﹣2t)cm,
故答案为:(18﹣2t);
(2)当OP=OQ时,则有18﹣2t=t,
解这个方程,得t=6,
即t=6时,能使OP=OQ;
(3)不能.理由如下:
设当t秒时点P追上点Q,则2t=t+18,
解这个方程,得t=18,
即点P追上点Q需要18s,此时点Q已经停止运动.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】某校八年级在一次广播操比赛中,三个班的各项得分如下表:
服装统一 | 动作整齐 | 动作准确 | |
八(1)班 | 80 | 84 | 87 |
八(2)班 | 97 | 78 | 80 |
八(3)班 | 90 | 78 | 85 |
(1) 填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是_________;在动作准确方面最有优势的是_________班
(2) 如果服装统一、动作整齐、动作准确三个方面按20%、30%、50%的比例计算各班的得分,请通过计算说明哪个班的得分最高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
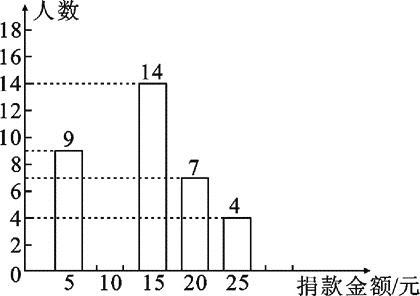
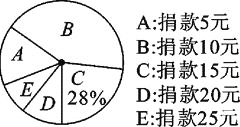
(1)本次共抽查学生________人,并将条形图补充完整;
(2)捐款金额的众数是________,平均数是________,中位数为________.
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
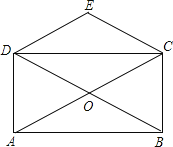
【题目】如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
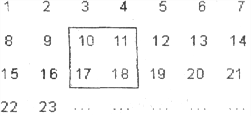
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com