Question

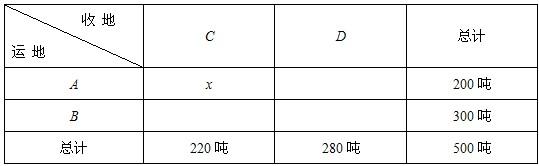
A城有化肥200吨，B城有化肥300吨，现要把这些化肥全部运到C、D两乡，从A城运往C、D两乡运化肥的费用分别为每吨20元和25元，从B城运往C、D两乡运化肥的费用分别为每吨15元和24元，现C乡需要化肥240吨，D乡需要化肥260吨，若A城运往C乡的化肥为x吨，总运费为y元．
（1）求y与x的函数关系；
（2）有多少种运化肥的方案；
（3）x为多少时，总运费最少？最少为多少元？并写出运费最低的方案．

Answer 1

解：（1）y=20x+25（200-x）+15（240-x）+24（60+x）=4x+10040；
（2）x可取0至200之间的任何数，所以有201中方案．
（3）因为y=4x+10040，y随x的增大而增大，
所以当x=0时，y最小，此时y=10040元．
此时的方案为：A城运往C乡的化肥为0吨，A城运往D乡的化肥为200吨，B城运往C乡的化肥为240吨，B城运往D乡的化肥为60吨．
分析：（1）A城运往C乡的化肥为x吨，则可得A城运往D乡的化肥为200-x吨，B城运往C乡的化肥为240-x吨，B城运往D乡的化肥为300-（240-x）吨，从而可得出y与x大的函数关系．
（2）x可取0至200之间的任何数，所以有201中方案．
点评：本题考查一次函数的应用，属于一般的应用题，解答本题的关键是根据题意得出y与x的函数关系式，另外同学们要掌握运用函数的增减性来判断函数的最值问题．