
分析 (1)将(1,-$\frac{1}{2}$)和点(-1,-$\frac{5}{2}$)代入y=ax2+bx-1求出a与b的值.
(2)先将抛物线C2为y=-$\frac{1}{2}$(x-h)2+k,由题意可知k=10,然后令y=0,求出A、B、C,然后根据勾股定理求出h的值即可.
解答 解:(1)(1,-$\frac{1}{2}$)和点(-1,-$\frac{5}{2}$)代入y=ax2+bx-1,
∴$\left\{\begin{array}{l}{-\frac{1}{2}=a+b-1}\\{-\frac{5}{2}=a-b-1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+x-1
(2)抛物线C1为:y=-$\frac{1}{2}$(x-1)2-$\frac{1}{2}$
设抛物线C2的解析式为:y=-$\frac{1}{2}$(x-h)2+k
∵由平移后抛物线的顶点纵坐标是10,
∴k=10,
令y=0代入y=-$\frac{1}{2}$(x-h)2+10,
∴x=h±2$\sqrt{5}$
∴A(h+2$\sqrt{5}$,0),B(h-2$\sqrt{5}$,0)
∴AB=4$\sqrt{5}$
令x=0代入y=-$\frac{1}{2}$(x-h)2+10,
∴y=10-$\frac{1}{2}$h2,
∴C(0,10-$\frac{1}{2}$h2)
∴AC2=(h+2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2
BC2=(h-2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2
当A为直角顶点时,
由勾股定理可知:BC2=AB2+AC2,
∴(h-2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2=80+(h+2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2
∴解得:h=-2$\sqrt{5}$,
当B是直角顶点时,
由勾股定理可知:AC2=AB2+BC2,
∴(h+2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2=80+(h-2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2
∴解得:h=2$\sqrt{5}$
当C是直角顶点时,
由勾股定理可知:AB2=AC2+BC2,
∴80=(h+2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2+(h-2$\sqrt{5}$)2+(-10+$\frac{1}{2}$h2)2
化简为:$\frac{1}{2}$h4-18h2+160=0,
∴解得:h2=20或h2=16,
∴h=±2$\sqrt{5}$,h=±4,
综上所述,抛物线C2的解析式为:y=-$\frac{1}{2}$(x±2$\sqrt{5}$)2+k或y=-$\frac{1}{2}$(x±4)2+k
点评 本题考查二次函数的综合问题,涉及勾股定理,一元二次方程的解法,待定系数法求解析式,本题综合较高,综合考查学生的灵活运用知识的能力.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m+1}{n}$ | B. | $\frac{m+1}{n+1}$ | C. | $\frac{m}{n+m}$ | D. | $\frac{m-n}{n-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A,B两地相距80km,甲、乙两人沿同一公路从A地出发到B的,甲骑摩托车,乙骑自行车,图中DE,OC分别表示离开A地的路程s(km)与运动时间t(h)的函数关系的图象.
已知A,B两地相距80km,甲、乙两人沿同一公路从A地出发到B的,甲骑摩托车,乙骑自行车,图中DE,OC分别表示离开A地的路程s(km)与运动时间t(h)的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
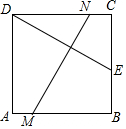 如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.
如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com