
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
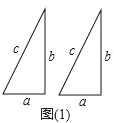
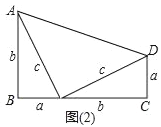
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
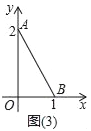
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
【答案】(1)证明见解析;(2)画图见解析,周长为![]() ;(3)①作图见解析;②(
;(3)①作图见解析;②( ![]() ,0),(0,
,0),(0, ![]() )(答案不唯一).
)(答案不唯一).
【解析】试题分析:(1)由图知,梯形的面积等于三个直角三角形的面积之和,用字母表示出来,化简后,即证明勾股定理;
(2)由a与b的值,利用勾股定理求出c的值,拼图后可知如图1所示时周长最大,求出最大周长即可;
(3)①分别以A、B为圆心,AB长为半径画圆,圆与坐标轴的交点即为满足条件的点,再作线段AB的垂直平分线,垂直平分线与坐标轴的交点也是满足条件的点;
②根据①所作的图形即可得.
试题解析:(1)由图可得, ![]() ×(a+b)(a+b)=
×(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2;
(2)当a=2,b=4时,可得:c=![]() ,
,
如图1时:四边形的周长为:8+4![]() ;
;
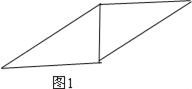
如图2时,四边形的周长为:12;
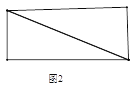
如图3时,四边形的周长为:4+4![]() ;
;

综上,图1是周长最大的四边形,周长为:8+4![]() ;
;
(3)①如图所示;
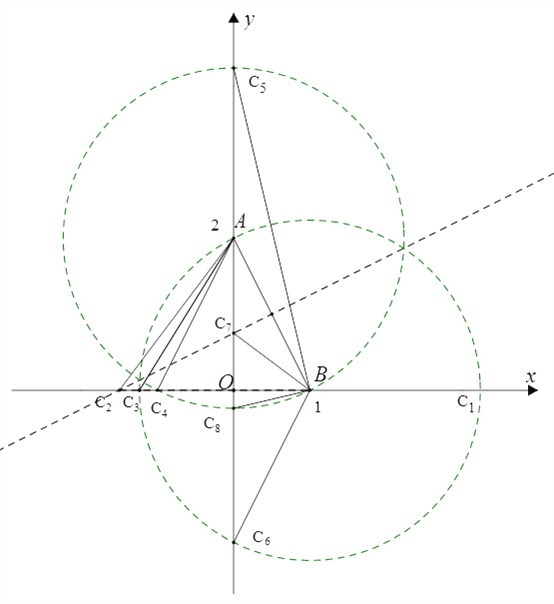
②如上图:
一个满足条件的在x轴上的点的坐标:如C3(﹣1,0);
一个满足条件的在y轴上的点的坐标:如C5(0,2+![]() ).
).
故答案为:(﹣1,0);(0,2+![]() )(答案不唯一).
)(答案不唯一).


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长度为8厘米的木棍截成三段,每段长度均为整数厘米.如果截成的三段木棍长度分别相同算作同一种截法(如:5,2,1和1,5,2),那么截成的三段木棍能构成三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算: ![]()
【答案】![]()
【解析】根据实数的运算顺序,利用二次根式性质,零指数幂法则,首先计算乘方、开方,然后从左向右依次计算.
解:原式=![]() .
.
“点睛”此题主要考查了实数的运算,在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
【题型】解答题
【结束】
22
【题目】已知4x2+y2 -4x-6y+10=0,求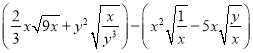 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°. 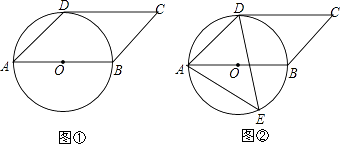
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com