
【题目】已知开口向上的抛物线y=ax2﹣2ax+3,在此抛物线上有A(﹣0.5,y1),B(2,y2)和C(3,y3)三点,则y1,y2和y3的大小关系为_____.
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,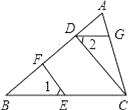
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. 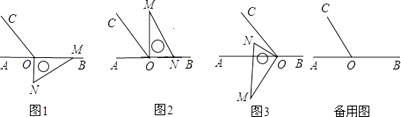
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 | 空调 | 彩电 | 冰箱 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当△BCP的面积最大时,求点P的坐标和△BCP的最大面积.
(3)当△BCP的面积最大时,在抛物线上是否点Q(异于点P),使△BCQ的面积等于△BCP,若存在,求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内点A在点D的左侧.
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G,

(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com