
【题目】如图,二次函数y=﹣mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内点A在点D的左侧.
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.

【答案】(1)y=﹣![]() x2+2;(2)p=﹣(x+2)2+8,其中﹣2<x<2;(3)不存在,证明见解析
x2+2;(2)p=﹣(x+2)2+8,其中﹣2<x<2;(3)不存在,证明见解析
【解析】试题分析: (1)由顶点坐标(0,2)可直接代入y=﹣mx2+4m,求得m=![]() ,即可求得抛物线的解析式;(2)由图及四边形ABCD为矩形可知AD∥x轴,长为2x的据对值,AB的长为A点的总坐标,由x与y的关系,可求得p关于自变量x的解析式,因为矩形ABCD在抛物线里面,所以x小于0,大于抛物线与x负半轴的交点;(3)由(2)得到的p关于x的解析式,可令p=9,求x的方程,看x是否有解,有解则存在,无解则不存在,显然不存在这样的p.
,即可求得抛物线的解析式;(2)由图及四边形ABCD为矩形可知AD∥x轴,长为2x的据对值,AB的长为A点的总坐标,由x与y的关系,可求得p关于自变量x的解析式,因为矩形ABCD在抛物线里面,所以x小于0,大于抛物线与x负半轴的交点;(3)由(2)得到的p关于x的解析式,可令p=9,求x的方程,看x是否有解,有解则存在,无解则不存在,显然不存在这样的p.
试题解析:
(1)∵二次函数y=﹣mx2+4m的顶点坐标为(0,2),
∴4m=2,
即m=![]() ,
,
∴抛物线的解析式为:y=﹣![]() x2+2;
x2+2;
(2)∵A点在x轴的负方向上坐标为(x,y),四边形ABCD为矩形,BC在x轴上,
∴AD∥x轴,
又∵抛物线关于y轴对称,
∴D、C点关于y轴分别与A、B对称.
∴AD的长为2x,AB长为y,
∴周长p=2y+4x=2(﹣![]() x2+2)﹣4x=﹣(x+2)2+8.
x2+2)﹣4x=﹣(x+2)2+8.
∵A在抛物线上,且ABCD组成矩形,
∴x<2,
∵四边形ABCD为矩形,
∴y>0,
即x>﹣2.
∴p=﹣(x+2)2+8,其中﹣2<x<2.
(3)不存在,
证明:假设存在这样的p,即:
9=﹣(x+2)2+8,
解此方程得:x无解,所以不存在这样的p.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )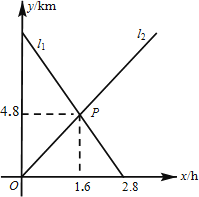
A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向上的抛物线y=ax2﹣2ax+3,在此抛物线上有A(﹣0.5,y1),B(2,y2)和C(3,y3)三点,则y1,y2和y3的大小关系为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于x的方程中,一定是一元二次方程的为( )
A. ax2+bx+c=0B. x2 -2=(x+3)2C. x2 +3y 5=0D. x2-1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形一边的平方为2(m2+1),其余两边分别为m-1,m + l,那么这个三角形是( );
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c,若a2+b2=c2 , 则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:写出二元一次方程x﹣3y=6的几个解: ![]() ,
, ![]() ,
, ![]() ,…,发现这些解的一般形式可表示为
,…,发现这些解的一般形式可表示为 ![]() (m为有理数).把一般形式再变形为
(m为有理数).把一般形式再变形为  ,可得
,可得 ![]() =y+2,整理得原方程x﹣3y=6.根据阅读材料解答下列问题:若二元一次方程ax+by=c的解,可以写成
=y+2,整理得原方程x﹣3y=6.根据阅读材料解答下列问题:若二元一次方程ax+by=c的解,可以写成 ![]() (n为有理数),则a+b+c= .
(n为有理数),则a+b+c= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com