
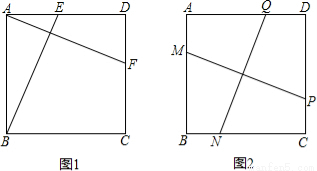
如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
(1)证明见解析;(2)MP与NQ相等,理由见解析.
【解析】
试题分析:(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;
(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.
试题解析:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,
∵在△ABE和△DAF中,
 ,
,
∴△ABE≌△DAF(ASA),
∴AF=BE;
(2)【解析】
MP与NQ相等.
理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
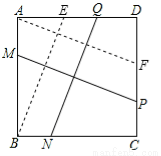
∵AB∥CD,AD∥BC,
∴四边形AMPF与四边形BNQE是平行四边形,
∴AF=PM,BE=NQ,
∴在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,
∵在△ABE和△DAF中,
 ,
,
∴△ABE≌△DAF(ASA),
∴AF=BE;
∴MP=NQ.
考点:1.正方形的性质;2.全等三角形的判定与性质.


科目:初中数学 来源:2015届甘肃省八年级下学期期末考试数学试卷(解析版) 题型:填空题
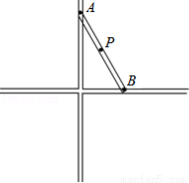
著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为 cm.
查看答案和解析>>
科目:初中数学 来源:2015届湖南长沙麓山国际实验学校八年级下学期期中数学试卷(解析版) 题型:选择题
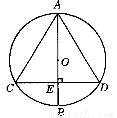
如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是( )
A.CE=DE B. =
= C.∠BAC=∠BAD D.OE=BE
C.∠BAC=∠BAD D.OE=BE
查看答案和解析>>
科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:填空题
在女子3000米的长跑中,运动员的平均速度v=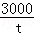 ,则这个关系式中自变量是 _________ .
,则这个关系式中自变量是 _________ .
查看答案和解析>>
科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列函数中一次函数的个数为( )
①y=2x;②y=3+4x;③y=;④2x+3y﹣1=0.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2015届湖北随州府河镇中心校八年级下学期期中考试数学试卷(解析版) 题型:解答题
已知x=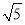 +3, y=
+3, y=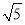 -3,求下列各式的值;
-3,求下列各式的值;
(1)x2-2xy+y2 ,
(2)x2-y2;
查看答案和解析>>
科目:初中数学 来源:2015届湖北随州府河镇中心校八年级下学期期中考试数学试卷(解析版) 题型:填空题
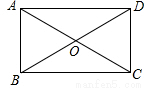
在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB=______________
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:解答题
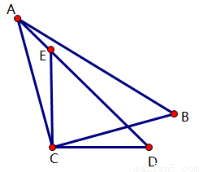
如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE的延长线上,求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com