
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
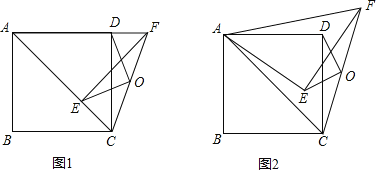
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
【答案】(1)![]() ,
,![]() ,理由见解析;(2)当
,理由见解析;(2)当![]() 时,(1)中的结论成立,理由见解析;(3)点O经过的路径长为
时,(1)中的结论成立,理由见解析;(3)点O经过的路径长为![]() .
.
【解析】
(1)根据直角三角形斜边上的中线等于斜边一半的性质可得OD与OE的数量关系;根据旋转的性质和正方形的性质可得AC=AF以及△ACF各内角的度数,进一步即可求出∠COE与∠DOF的度数,进而可得OD与OE的位置关系;
(2)延长EO到点M,使![]() ,连接DM、CM、DE,如图2所示,先根据SAS证明
,连接DM、CM、DE,如图2所示,先根据SAS证明![]() ≌
≌![]() ,得
,得![]() ,
,![]() ,再根据正方形的性质和旋转的性质推得
,再根据正方形的性质和旋转的性质推得![]() ,进一步在△ACF中根据三角形内角和定理和正方形的性质得出
,进一步在△ACF中根据三角形内角和定理和正方形的性质得出![]() ,再一次运用SAS推出
,再一次运用SAS推出![]() ≌
≌![]() ,于是
,于是![]() ,进一步即可得出OE、OD的位置关系,然后再运用SAS推出
,进一步即可得出OE、OD的位置关系,然后再运用SAS推出![]() ≌
≌![]() ,即可得OD与OE的数量关系;
,即可得OD与OE的数量关系;
(3)连接AO,如图3所示,先根据等腰三角形三线合一的性质得出![]() ,即可判断点O的运动路径,由
,即可判断点O的运动路径,由![]() 可得点O经过的路径长,进一步即可求得结果.
可得点O经过的路径长,进一步即可求得结果.
解:(1)![]() ,
,![]() ;理由如下:
;理由如下:
由旋转的性质得:![]() ,
,![]() ,
,
∵四边形ABCD是正方形,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,O为CF的中点,∴
,O为CF的中点,∴![]() ,
,
同理:![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)当![]() 时,(1)中的结论成立,理由如下:
时,(1)中的结论成立,理由如下:
延长EO到点M,使![]() ,连接DM、CM、DE,如图2所示:
,连接DM、CM、DE,如图2所示:
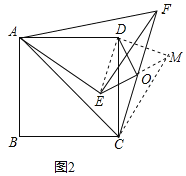
∵O为CF的中点,∴![]() ,
,
在![]() 和
和![]() 中,
中,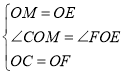 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() ,
,![]() .
.
∵四边形ABCD是正方形,∴![]() ,
,![]() ,
,
∵![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,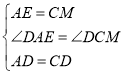 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,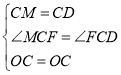 ,
,
∴![]() ≌
≌![]() (SAS),∴
(SAS),∴![]() .
.
∴![]() ,∴
,∴![]() ,
,![]() ;
;
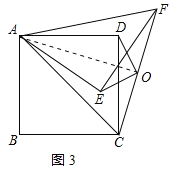
(3)连接AO,如图3所示:
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴点O在以AC为直径的圆上运动,
∵![]() ,∴点O经过的路径长等于以AC为直径的圆的周长,
,∴点O经过的路径长等于以AC为直径的圆的周长,
∵![]() ,∴点O经过的路径长为:
,∴点O经过的路径长为:![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
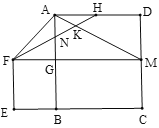
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法,下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.
问题情境:在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() .以
.以![]() 为旋转中心,将线段
为旋转中心,将线段![]() 顺时针旋转,旋转角与
顺时针旋转,旋转角与![]() 相等,得到线段
相等,得到线段![]() ,连接
,连接![]() .
.
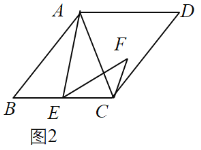
(1)特例如图1,若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 位置关系是_________.此时可以过点
位置关系是_________.此时可以过点![]() 作
作![]() 的平行线来对结论进行证明(这里不要求证明)
的平行线来对结论进行证明(这里不要求证明)
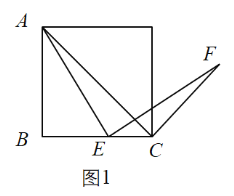
(2)拓展探究:如图2,若四边形![]() 是菱形,当
是菱形,当![]() 时,求
时,求![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
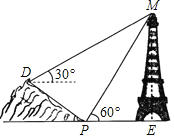
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=![]() ,请你帮助小明计算古塔的高度ME.(结果保留根号)
,请你帮助小明计算古塔的高度ME.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴分别相交于A,B两点,与反比例函数
与x轴、y轴分别相交于A,B两点,与反比例函数![]() 在第二象限内交于点C,且点B是
在第二象限内交于点C,且点B是![]() 的中点.
的中点.
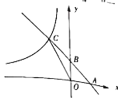
(1)求点C的坐标及k的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形的面积为96000000cm2,第一次截去它的![]() ,第二次截去剩下的
,第二次截去剩下的![]() ,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
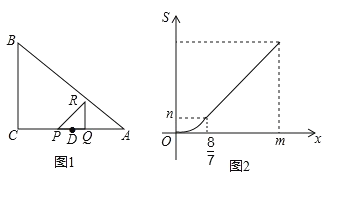
【题目】如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2.点P、Q同时从D点出发,以相同的速度分别沿射线DC、射线DA运动.过点Q作AC的垂线段QR,使QR=PQ,联接PR.当点Q到达A时,点P、Q同时停止运动.设PQ=x.△PQR和△ABC重合部分的面积为S.S关于x的函数图像如图2所示(其中0<x≤![]() ,
,![]() <x≤m时,函数的解析式不同)
<x≤m时,函数的解析式不同)
(1)填空:n的值为___________;
(2)求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别为A(﹣3,3),B(﹣5,2),C(﹣1,1).
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2,且ABC位于点C的异侧,并表示出点A1的坐标.
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
(3)在(2)的条件下求出点B经过的路径长(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com