
【题目】一个矩形的面积为96000000cm2,第一次截去它的![]() ,第二次截去剩下的
,第二次截去剩下的![]() ,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
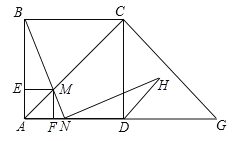
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
(1)当AM=_____________时,△ABM是以AB为底边的等腰三角形;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S与t的函数关系式,并求S最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月16日扬州首批为民服务5G站点正式上线,自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
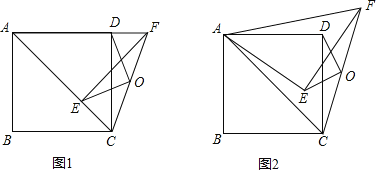
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
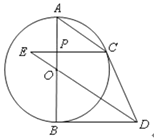
【题目】如图,AB是⊙O的直径,DB切⊙O于点B,C是圆上一点,过点C作AB的垂线,交AB于点P,与DO的延长线交与点E,且ED∥AC,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=12,OP:AP=1:2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研发了一种新药,试验药效时发现:1.5小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax2+bx表示;1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=![]() (k>0)表示,部分实验数据如表:
(k>0)表示,部分实验数据如表:
时间x(小时) | 0.2 | 1 | 1.8 | … |
含药量y(微克) | 7.2 | 20 | 12.5 | … |
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(![]() ≈1.41,精确到0.1小时)
≈1.41,精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
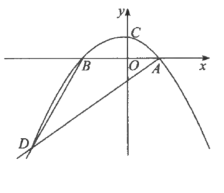
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且经过点
,且经过点![]() ,连接
,连接![]() .
.
(1)求该抛物线的函数关系式;
(2)△ANM与![]() 是否相似?若相似,请求出此时点
是否相似?若相似,请求出此时点![]() 、点
、点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 重合),过
重合),过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,则⊙
,则⊙![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于 .(直接写出答案)
上所截得的线段长度的最大值等于 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学具专卖店试销一种成本为60元/套的学具.规定试销期间销售单价不得低于成本单价,且获利不得高于成本价的20%,该专卖店每天的固定费用是100元.试销发现,每件销售单价相对成本提高x元(x为整数)与日平均销售量y件之间符合一次函数关系,且当x=10时,y=40;x=25时,y=10.
(1)求y与x之间的关系式;
(2)该学具专卖店日平均获得毛利润为w元(毛利润=利润﹣固定费用),求当销售单价为多少元时,日平均毛利润最大,最大日平均毛利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
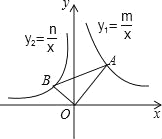
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )
A.m=![]() nB.m=﹣
nB.m=﹣![]() nC.m=﹣
nC.m=﹣![]() nD.m=﹣3n
nD.m=﹣3n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com