
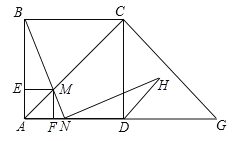
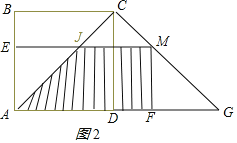
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
(1)当AM=_____________时,△ABM是以AB为底边的等腰三角形;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S与t的函数关系式,并求S最大值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)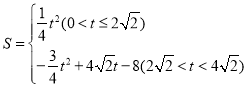 ,当t=
,当t=![]() 时,S的最大值是
时,S的最大值是![]() .
.
【解析】
(1)△ABM是以AB为底边的等腰三角形,则![]() 为正方形的对角线的交点,从而可得答案,
为正方形的对角线的交点,从而可得答案,
(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;
(3)①当M在AC上时,即0<t≤![]() 时,△AMF为等腰直角三角形,得出AF=FM=
时,△AMF为等腰直角三角形,得出AF=FM=![]() 求出S=
求出S=![]() AFFM=
AFFM=![]() ;当t=
;当t=![]() 时,即可求出S的最大值; ②当M在CG上时,即
时,即可求出S的最大值; ②当M在CG上时,即![]() <t<
<t<![]() 时,先证明△ACD≌△GCD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=
时,先证明△ACD≌△GCD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=![]() ,得出S=S△ACG-S△CMJ-S△FMG.
,得出S=S△ACG-S△CMJ-S△FMG.
解:(1)![]() △ABM是以AB为底边的等腰三角形,
△ABM是以AB为底边的等腰三角形,
![]()
此时点M为AC的中点,
![]() 正方形ABCD,
正方形ABCD,![]()
![]()
![]()
故答案为:![]()
(2)在AB上截取AK=AN,连接KN;
![]() 正方形ABCD,
正方形ABCD,
![]() ∠ADC=90°,AB=AD,∠CDG=90°,
∠ADC=90°,AB=AD,∠CDG=90°,![]()
![]() BK=DN,
BK=DN,
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]() △BNK≌△NHD,
△BNK≌△NHD,
![]() BN=NH;
BN=NH;
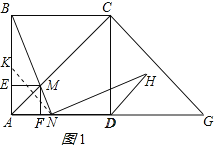
(3)①当点M在AC上时,即0<t≤![]() 时,
时,
由正方形的性质得:△AMF为等腰直角三角形.
∵AM=t,
∴AF=FM=![]()
∴S=![]() AFFM=
AFFM= ![]()
当![]() 时,
时,![]()
当点M在CG上时,
即![]() <t<
<t<![]() 时,CM=
时,CM=![]() ,MG=
,MG=![]() .
.
∵AD=DG,∠ADC=∠CDG,CD=CD,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°
∴∠ACM=∠ACD+∠GCD=90°
∴∠G=90-∠GCD=90°-45°=45°
∴△MFG为等腰直角三角形.
∴FG=![]() ,
,
∴S=S△ACG-S△MCJ-S△FMG=![]()
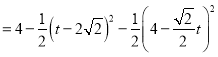
![]()
当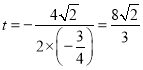 ,
,
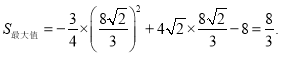
综上:当![]()
![]()
∴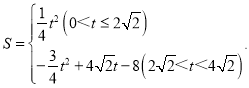


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
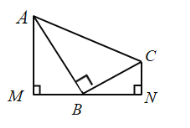
(1)如图.分别过![]() 、
、![]() 两点作经过点
两点作经过点![]() 的直线的垂线,垂足分别为
的直线的垂线,垂足分别为![]() 、
、![]() ,求证:
,求证:![]() .
.
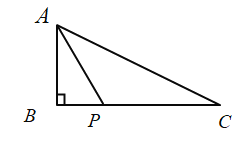
(2)如图,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,求
,求![]() 的值.
的值.
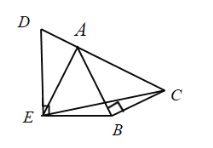
(3)如图,![]() 是边
是边![]() 延长线上一点,
延长线上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
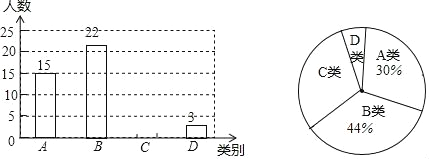
【题目】某校为了解本校九年级学生物理实验操作技能考查的备考情况,随机抽取该年级部分学生进行了一次测试,并根据中考标准按测试成绩分成A、B、C、D四个等级,绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取参加测试的学生为_____人,扇形统计图中A等级所对的圆心角是____度;
(2)请补全条形统计图和扇形统计图;
(3)若该校九年级男生有300人,请估计该校九年级学生物理实验操作成绩为C等级的有____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
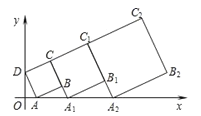
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2020个正方形的面积是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
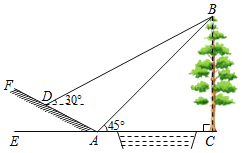
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
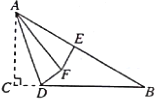
【题目】如图,已知在△ABC中,![]() ,
,![]() ,
,![]() ,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
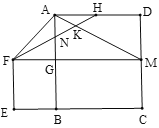
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形的面积为96000000cm2,第一次截去它的![]() ,第二次截去剩下的
,第二次截去剩下的![]() ,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
,如此截下去,第六次截去后剩余图形的面积为_____cm2,用科学记数法表示剩余图形的面积为_____cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com