
【题目】在![]() 中,
中,![]() .
.
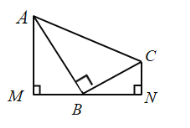
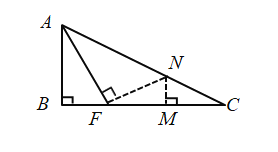
(1)如图.分别过![]() 、
、![]() 两点作经过点
两点作经过点![]() 的直线的垂线,垂足分别为
的直线的垂线,垂足分别为![]() 、
、![]() ,求证:
,求证:![]() .
.
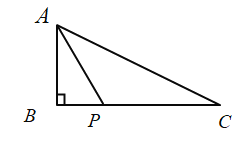
(2)如图,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,求
,求![]() 的值.
的值.
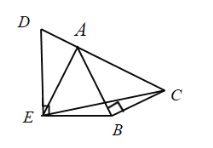
(3)如图,![]() 是边
是边![]() 延长线上一点,
延长线上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)见解析 (2)![]() (3)
(3)![]()
【解析】
(1)由题意,只要证明△AMB∽△BNC,即可得到结论成立;
(2)过![]() 点作
点作![]() 交
交![]() 于
于![]() 点,过
点,过![]() 作
作![]() 于
于![]() 点,先证明
点,先证明![]() ,得到
,得到![]() ,再证明
,再证明![]() ,即可得到结论成立;
,即可得到结论成立;
(3)作AG⊥BE于G,作CH⊥BE于点H,先判断出![]() ,再同(2)的方法,即可得出结论.
,再同(2)的方法,即可得出结论.
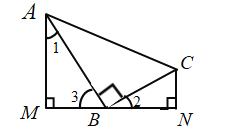
证明:(1):![]() ,
,
![]() ,
,
又![]() ,
,
∴∠M=∠N=90°,∠1+∠3=90°,
∴∠1=∠2.
![]() ,
,
![]() ;
;
(2)过![]() 点作
点作![]() 交
交![]() 于
于![]() 点,过
点,过![]() 作img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/04/8078862f/SYS202007220422182855736715_DA/SYS202007220422182855736715_DA.007.png" width="72" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于
作img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/04/8078862f/SYS202007220422182855736715_DA/SYS202007220422182855736715_DA.007.png" width="72" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于![]() 点,
点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,![]()
又![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
解得:![]() ,
,
![]() ;
;
(3)如图,作AG⊥BE于G,作CH⊥BE于点H,
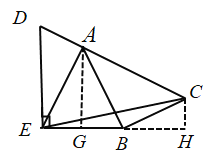
在Rt△ABC中,![]() ,
,
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
同(1)的方法得,△ABG∽△BCH
∴![]() ,
,
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∴![]() ,
,
∴n=2m,
∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,
在Rt△CEH中,tan∠BEC=![]() .
.
∴![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
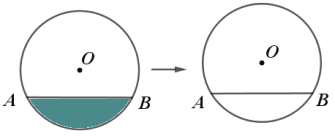
【题目】如图,![]() 是一个圆柱体污水管道的横截面,管道中有部分污水,污水液面横截面宽度(即
是一个圆柱体污水管道的横截面,管道中有部分污水,污水液面横截面宽度(即![]() 长)为
长)为![]() 污水管道直径为
污水管道直径为![]() 则弦
则弦![]() 所对圆周角的大小为_____________________
所对圆周角的大小为_____________________![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的与
的与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
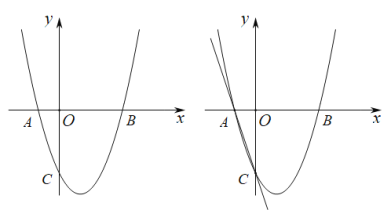
(1)求该抛物线的解析式及顶点的坐标;
(2)若![]() 是线段
是线段![]() 上一动点,过
上一动点,过![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 时,
时,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式;若
的函数关系式;若![]() 有最大值,请求出
有最大值,请求出![]() 的最大值,若没有,请说明理由;
的最大值,若没有,请说明理由;
(3)若![]() 是
是![]() 轴上一个动点,过
轴上一个动点,过![]() 作射线
作射线![]() 交抛物线于点
交抛物线于点![]() ,随着
,随着![]() 点的运动,在
点的运动,在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使以
,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请直接写出
为顶点的四边形为平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
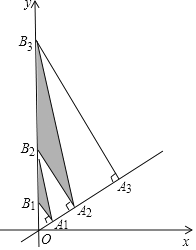
【题目】如图,直线![]() 上有点
上有点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别过点
分别过点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 作直线
作直线![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,依次连接
,依次连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,得到
,得到![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为_______.(用含有正整数
的面积为_______.(用含有正整数![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,∠ABC=60°,P、Q是对角线BD上的两个动点,点P从点D出发沿BD方向以1cm/s的速度向点B运动,运动终点为B;点Q从点B出发沿着BD的方向以2cm/s的速度向点D运动,运动终点为D.两点同时出发,设运动时间为x(s),以A、Q、C、P为顶点的图形面积为y(cm2),y与x的函数图像如图②所示,根据图像回答下列问题:
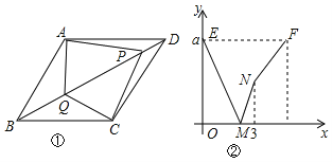
(1)BD= ,a= ;
(2)当x为何值时,以A、Q、C、P为顶点的图形面积为4![]() cm2?
cm2?
(3)在整个运动的过程中,若△AQP为直角三角形,请直接写出符合条件的所有x的值:.
查看答案和解析>>
科目:初中数学 来源: 题型:
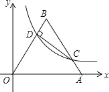
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )
A. 25![]() B. 18
B. 18![]() C. 9D. 9
C. 9D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
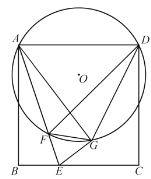
【题目】在正方形ABCD中,点E是BC边上一动点,连接AE,沿AE将△ABE翻折得△AGE,连接DG,作△AGD的外接⊙O,⊙O交AE于点F,连接FG、FD.
(1)求证∠AGD=∠EFG;
(2)求证△ADF∽△EGF;
(3)若AB=3,BE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
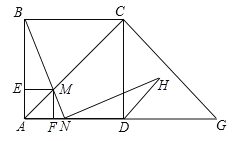
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
(1)当AM=_____________时,△ABM是以AB为底边的等腰三角形;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S与t的函数关系式,并求S最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com