
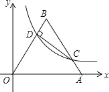
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )
A. 25![]() B. 18
B. 18![]() C. 9D. 9
C. 9D. 9![]()
【答案】D
【解析】
根据等边三角形的性质表示出D,C点坐标,进而利用反比例函数图象上点的坐标特征得出答案.
解:过点D作DE⊥x轴于点E,过C作CF⊥x轴于点F,如图所示.
可得:∠ODE=30∠BCD=30°,
设OE=a,则OD=2a,DE=![]() a,
a,
∴BD=OB﹣OD=10﹣2a,BC=2BD=20﹣4a,AC=AB﹣BC=4a﹣10,
∴AF=![]() AC=2a﹣5,CF=
AC=2a﹣5,CF=![]() AF=
AF=![]() (2a﹣5),OF=OA﹣AF=15﹣2a,
(2a﹣5),OF=OA﹣AF=15﹣2a,
∴点D(a,![]() a),点C[15﹣2a,
a),点C[15﹣2a,![]() (2a﹣5)].
(2a﹣5)].
∵点C、D都在双曲线y=![]() 上(k>0,x>0),
上(k>0,x>0),
∴a![]() a=(15﹣2a)×
a=(15﹣2a)×![]() (2a﹣5),
(2a﹣5),
解得:a=3或a=5.
当a=5时,DO=OB,AC=AB,点C、D与点B重合,不符合题意,
∴a=5舍去.
∴点D(3,3![]() ),
),
∴k=3×3![]() =9
=9![]() .
.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
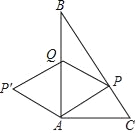
【题目】如图,在△ABC中,∠BAC=90°,AB=8cm,AC=6cm,动点P从点C出发沿CB方向以3cm/s的速度向点B运动,同时动点Q从点B出发沿BA方向以2cm/s的速度向点A运动,将△APQ沿直线AB翻折得△AP′Q,若四边形APQP′为菱形,则运动时间为( )
A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
查看答案和解析>>
科目:初中数学 来源: 题型:
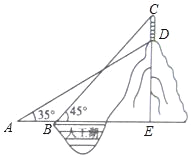
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,弦
,弦![]() 与
与![]() 交于点
交于点![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 为等腰三角形;
为等腰三角形;
(2)若![]() ,
,![]() 的半径为3,求
的半径为3,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数![]() 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数![]() 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
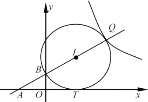
【题目】如图,在平面直角坐标系中,直线l:y=kx+1(k>0)与x轴、y轴分别相交于点A、B,tan∠ABO=![]() .
.
(1)求k的值;
(2)若直线l:y=kx+1与双曲线y=![]() (
(![]() )的一个交点Q在一象限内,以BQ为直径的⊙I与x轴相明于点T,求m的值.
)的一个交点Q在一象限内,以BQ为直径的⊙I与x轴相明于点T,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
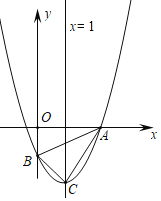
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点B,顶点为C.
与y轴交于点B,顶点为C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点P在x轴上,将线段BP绕着点P逆时针旋转
若点P在x轴上,将线段BP绕着点P逆时针旋转![]() 得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
得到PD,点D是否会落在抛物线上?如果会,求出点P的坐标;若果不会,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
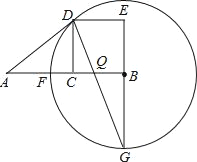
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com