
【题目】如图①,在菱形ABCD中,∠ABC=60°,P、Q是对角线BD上的两个动点,点P从点D出发沿BD方向以1cm/s的速度向点B运动,运动终点为B;点Q从点B出发沿着BD的方向以2cm/s的速度向点D运动,运动终点为D.两点同时出发,设运动时间为x(s),以A、Q、C、P为顶点的图形面积为y(cm2),y与x的函数图像如图②所示,根据图像回答下列问题:
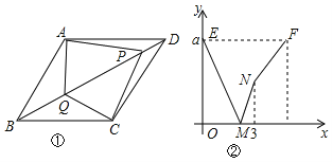
(1)BD= ,a= ;
(2)当x为何值时,以A、Q、C、P为顶点的图形面积为4![]() cm2?
cm2?
(3)在整个运动的过程中,若△AQP为直角三角形,请直接写出符合条件的所有x的值:.
【答案】(1)6,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,3,
,3,![]() 或4.
或4.
【解析】
(1)如图①中,连接![]() 交
交![]() 于点
于点![]() .由题意:点
.由题意:点![]() 的实际意义表示
的实际意义表示![]() 时,点
时,点![]() 运动到点
运动到点![]() ,由此求出
,由此求出![]() 即可解决问题;
即可解决问题;
(2)图②求出直线![]() ,直线
,直线![]() 的解析式即可解决问题;
的解析式即可解决问题;
(3)分三种情况讨论:当∠AQP=90°,∠APQ=90-°,∠QAP=90°时,求解即可.
解:(1)如图①中,连接![]() 交
交![]() 于点
于点![]() .
.

由题意:点![]() 的实际意义表示
的实际意义表示![]() 时,点
时,点![]() 运动到点
运动到点![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
故答案为:6,![]() ;
;
(2)设![]() 秒后
秒后![]() ,
,![]() 相遇.则
相遇.则![]() ,
,![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() .
.
(3)满足条件的![]() 的值为
的值为![]() ,3,
,3,![]() 或4.
或4.
△AQP为直角三角形,有三种情况:
I.当∠AQP=90°时,点![]() 运动到BD的中点
运动到BD的中点![]() (对角线的交点),
(对角线的交点),
![]() ,
,
∴![]() ,
,
II.当∠APQ=90°时,点![]() 运动到BD的中点
运动到BD的中点![]() (对角线的交点),
(对角线的交点),
![]()
∴![]() ,
,
III.当∠PAQ=90°时,有![]() ,
,
∵![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,解得:
,解得: ![]() (不合题意舍去)
(不合题意舍去)![]() ,
,
当![]() 时,此时
时,此时![]() 已经到达终点,所以,
已经到达终点,所以,![]() ,此时
,此时![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ;
;
综上所述,满足条件的![]() 的值为
的值为![]() ,3,
,3,![]() 或4.
或4.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的两条对角线相交于点
的两条对角线相交于点![]() 轴,垂足为点
轴,垂足为点![]() 正比例函数
正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 两点.
两点.

(1)求正比例函数和反比例函数的解析式;
(2)求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)的图象经过A(3,18)和B(﹣2,8)两点.
(1)求一次函数的解析式;
(2)若一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,求交点坐标.
(m≠0)的图象只有一个交点,求交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为( )
有两个不相等的实数根.其中结论正确的个数为( )
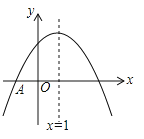
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
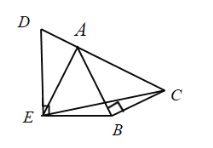
【题目】在![]() 中,
中,![]() .
.
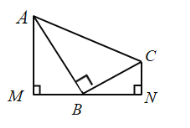
(1)如图.分别过![]() 、
、![]() 两点作经过点
两点作经过点![]() 的直线的垂线,垂足分别为
的直线的垂线,垂足分别为![]() 、
、![]() ,求证:
,求证:![]() .
.
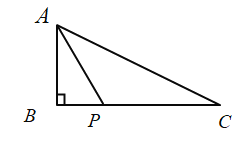
(2)如图,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,求
,求![]() 的值.
的值.
(3)如图,![]() 是边
是边![]() 延长线上一点,
延长线上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在校园艺术节期间举行学生书画大赛活动,准备购买甲、乙两种文具,奖励在活动中表现优秀的学生.已知购买2个甲种文具、1个乙种文具共需花费35元;购买1个甲种文具、3个乙种文具共需花费30元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共120个,投入资金不少于95元又不多于1000元,问有多少种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
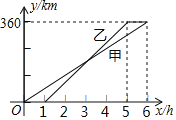
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲,y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h;
(2)当1≤x≤5时,求y乙关于x的函数关系式;
(3)当乙与A地相距240km时,直接写出甲与A地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
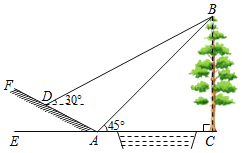
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com