
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为( )
有两个不相等的实数根.其中结论正确的个数为( )
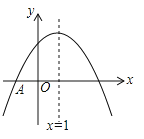
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】C
【解析】
根据抛物线图像的性质得到a的范围,根据对称轴和x轴上的点可得到两个等量关系,变形替换从而可以得到①②正确,根据顶点最高可得到③正确,由数形结合可得到④错误.
∵抛物线的开口向下
∴a<0
∵对称轴x=![]() =1
=1
∴b=2a
∴3a+b=a
∴3a+b<0,故①正确;
∵ A(1,0)在抛物线上
∴ab+c=0
∴3a +c=0
∴c=3a
∵c在2,3之间
∴2≤3a≤3
∴1≤a≤![]() ,故②正确;
,故②正确;
∵顶点坐标![]() ,且当x=1时,y有最大值,最大值为n
,且当x=1时,y有最大值,最大值为n
∴对于任意实数m,a+b+c≥am![]() +bm+c
+bm+c
∴a+b≥am![]() +bm ,故③正确
+bm ,故③正确
∵顶点坐标![]()
∴y=ax![]() +bx+c与y=n只有一个交点
+bx+c与y=n只有一个交点
∴y=ax![]() +bx+c与y=n+1没有交点,故④错误
+bx+c与y=n+1没有交点,故④错误
故选C


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
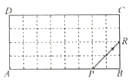
【题目】如图,在矩形![]() 中,
中,![]() ,一发光电子开始置于
,一发光电子开始置于![]() 边的点
边的点![]() 处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着
处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着![]() 方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于
方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于![]() ,当发光电子与矩形的边碰撞2020次后,它与
,当发光电子与矩形的边碰撞2020次后,它与![]() 边的碰撞次数是__________.
边的碰撞次数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
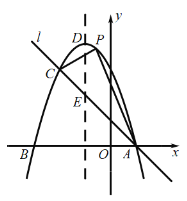
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,其中点
,其中点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,抛物线的顶点为点
,抛物线的顶点为点![]() .
.
(1)求抛物线和直线![]() 的解析式.
的解析式.
(2)若点![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 的面积的最大值及此时点
的面积的最大值及此时点![]() 的坐标.
的坐标.
(3)若抛物线的对称轴与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否为平行四边形?若能,求出点
为顶点的四边形能否为平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
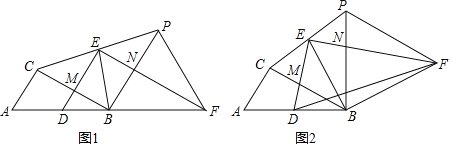
【题目】已知D是Rt△ABC斜边AB的中点,∠ACB=90°,∠ABC=30°,过点D作Rt△DEF使∠DEF=90°,∠DFE=30°,连接CE并延长CE到P,使EP=CE,连接BE,FP,BP,设BC与DE交于M,PB与EF交于N.
(1)如图1,当D,B,F共线时,求证:
①EB=EP;
②∠EFP=30°;
(2)如图2,当D,B,F不共线时,连接BF,求证:∠BFD+∠EFP=30°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书已知甲图书每本价格是乙图书每本价格的![]() 倍,用
倍,用![]() 元单独购买甲图书比用
元单独购买甲图书比用![]() 元单独购买乙图书要少
元单独购买乙图书要少![]() 本.
本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的![]() 倍少
倍少![]() 本,且用于购买甲、乙两种图书的总经费不超过
本,且用于购买甲、乙两种图书的总经费不超过![]() 元,那么该图书馆最多可以购买多少本乙图书?
元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,∠ABC=60°,P、Q是对角线BD上的两个动点,点P从点D出发沿BD方向以1cm/s的速度向点B运动,运动终点为B;点Q从点B出发沿着BD的方向以2cm/s的速度向点D运动,运动终点为D.两点同时出发,设运动时间为x(s),以A、Q、C、P为顶点的图形面积为y(cm2),y与x的函数图像如图②所示,根据图像回答下列问题:
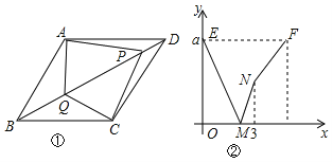
(1)BD= ,a= ;
(2)当x为何值时,以A、Q、C、P为顶点的图形面积为4![]() cm2?
cm2?
(3)在整个运动的过程中,若△AQP为直角三角形,请直接写出符合条件的所有x的值:.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ、PB、QC是⊙O的切线,切点分别为A、B、C,点D在![]() 上,若∠D=100°,则∠P与∠Q的度数之和是( )
上,若∠D=100°,则∠P与∠Q的度数之和是( )
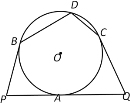
A.160°B.140°C.120°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
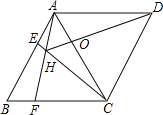
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com