
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,其中点
,其中点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,抛物线的顶点为点
,抛物线的顶点为点![]() .
.
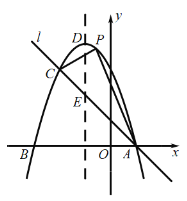
(1)求抛物线和直线![]() 的解析式.
的解析式.
(2)若点![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 的面积的最大值及此时点
的面积的最大值及此时点![]() 的坐标.
的坐标.
(3)若抛物线的对称轴与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否为平行四边形?若能,求出点
为顶点的四边形能否为平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)y=-x2-2x+3,y=-x+1;(2)最大值为![]() ,此时点P(
,此时点P(![]() ,
,![]() );(3)能,(0,1),(
);(3)能,(0,1),(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)直接利用待定系数法进行求解,即可得到答案;
(2)设点P(m,-m2-2m+3),则Q(m,-m+1),求出PQ的长度,结合三角形的面积公式和二次函数的性质,即可得到答案;
(3)根据题意,设点M(t,-t+1),则点N(t,-t2-2t+3),可分为两种情况进行①当点M在线段AC上时,点N在点M上方;②当点M在线段AC(或CA)延长线上时,点N在点M下方;分别求出点M的坐标即可.
解:(1)∵抛物线y=-x2+bx+c过点A(1,0),C(-2,3),
∴![]() 解得:
解得:![]()
∴抛物线的解析式为y=-x2-2x+3.
设直线AC的解析式为y=kx+n.
将点A,C坐标代入,得
![]() 解得
解得![]()
∴直线AC的解析式为y=-x+1.
(2)过点P作PQ∥y轴交AC于点Q.
设点P(m,-m2-2m+3),则Q(m,-m+1).
∴PQ=(-m2-2m+3)-(-m+1)=-m2-m+2.
∴S△APC=S△PCQ+S△APQ=![]() PQ·(xA-xC)=
PQ·(xA-xC)=![]() (-m2-m+2)×3=
(-m2-m+2)×3=![]() .
.
∴当m=![]() 时,S△APC最大,最大值为
时,S△APC最大,最大值为![]() ,此时点P(
,此时点P(![]() ,
,![]() ).
).
(3)能.
∵y=-x2-2x+3,点D为顶点,
∴点D(-1,4),
令x=-1时,y=-(-1)+1=2,
∴点E(-1,2).
∵MN∥DE,
∴当MN=DE=2时,以D,E,M,N为顶点的四边形是平行四边形.
∵点M在直线AC上,点N在抛物线上,
∴设点M(t,-t+1),则点N(t,-t2-2t+3).
①当点M在线段AC上时,点N在点M上方,则
MN=(-t2-2t+3)-(-t+1)=-t2-t+2.
∴-t2-t+2=2,
解得:t=0或t=-1(舍去).
∴此时点M的坐标为(0,1).
②当点M在线段AC(或CA)延长线上时,点N在点M下方,则
MN=(-t+1)-(-t2-2t+3)=t2+t-2.
∴t2+t-2=2,
解得:t=![]() 或t=
或t=![]() .
.
∴此时点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
综上所述,满足条件的点M的坐标为:(0,1),(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的两条对角线相交于点
的两条对角线相交于点![]() 轴,垂足为点
轴,垂足为点![]() 正比例函数
正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 两点.
两点.

(1)求正比例函数和反比例函数的解析式;
(2)求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() 、
、![]() 两点.
两点.
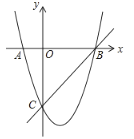
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥(英文名称:Hong Kong-Zhuhai-Macao Bridge)是中国境内一座连接香港、广东珠海和澳门的桥隧工程,位于中国广东省珠江口伶洋海域内,为珠江三角洲地区环线高速公路南环段.港珠澳大桥于![]() 年
年![]() 月
月![]() 日动工建设;于
日动工建设;于![]() 年
年![]() 月
月![]() 日实现主体工程全线贯通;于
日实现主体工程全线贯通;于![]() 年
年![]() 月
月![]() 日完成主体工程验收;同年
日完成主体工程验收;同年![]() 月
月![]() 日上午
日上午![]() 时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
项目 | 内容 | ||
课题 | 测量港珠澳大桥某一段斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧斜拉索 | |
测量数据 |
|
|
|
|
|
| |
|
| ||

(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点![]() 到
到![]() 的距离(参考数据:
的距离(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的等腰直角三角形放置在平面直角坐标系中,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
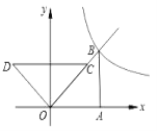
(1)求反比例函数的解析式;
(2)把![]() 沿射线
沿射线![]() 移动,当点
移动,当点![]() 落在
落在![]() 图象上的
图象上的![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)的图象经过A(3,18)和B(﹣2,8)两点.
(1)求一次函数的解析式;
(2)若一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,求交点坐标.
(m≠0)的图象只有一个交点,求交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),则下列结论:①
之间(包含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为( )
有两个不相等的实数根.其中结论正确的个数为( )
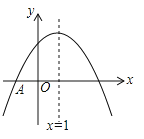
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
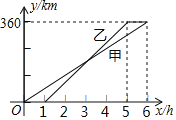
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲,y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h;
(2)当1≤x≤5时,求y乙关于x的函数关系式;
(3)当乙与A地相距240km时,直接写出甲与A地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com