
【题目】如图,两个全等的等腰直角三角形放置在平面直角坐标系中,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
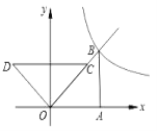
(1)求反比例函数的解析式;
(2)把![]() 沿射线
沿射线![]() 移动,当点
移动,当点![]() 落在
落在![]() 图象上的
图象上的![]() 时,求点
时,求点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
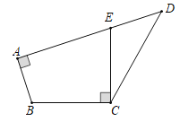
【题目】(1)如图,一块四边形纸板剪去![]() ,得到四边形
,得到四边形![]() ,测得
,测得![]() ,
,![]() ,
,![]() .能否在四边形纸板
.能否在四边形纸板![]() 上只剪一刀,使剪下的三角形与
上只剪一刀,使剪下的三角形与![]() 全等?请说明理由.
全等?请说明理由.
(2)我市某学校八年级同学乘坐大巴车去长江青少年素质教育实践基地参加综合实践活动.1号车出发4分钟后,2号车才出发,结果两车同时到达.已知素质教育基地距离该校18千米,2号车的平均速度是1车的平均速度的![]() 倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,其中点
,其中点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,抛物线的顶点为点
,抛物线的顶点为点![]() .
.
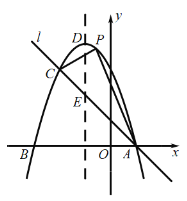
(1)求抛物线和直线![]() 的解析式.
的解析式.
(2)若点![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 的面积的最大值及此时点
的面积的最大值及此时点![]() 的坐标.
的坐标.
(3)若抛物线的对称轴与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否为平行四边形?若能,求出点
为顶点的四边形能否为平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3﹣(n2+1)x+n=x3﹣n2x﹣x+n=x(x2﹣n2)﹣(x﹣n)=x(x﹣n)(x+n)﹣(x﹣n)=(x﹣n)(x2+nx﹣1).
理解运用:如果x3﹣(n2+1)x+n=0,那么(x﹣n)(x2+nx﹣1)=0,即有x﹣n=0或x2+nx﹣1=0,
因此,方程x﹣n=0和x2+nx﹣1=0的所有解就是方程x3﹣(n2+1)x+n=0的解.
解决问题:求方程x3﹣5x+2=0的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知D是Rt△ABC斜边AB的中点,∠ACB=90°,∠ABC=30°,过点D作Rt△DEF使∠DEF=90°,∠DFE=30°,连接CE并延长CE到P,使EP=CE,连接BE,FP,BP,设BC与DE交于M,PB与EF交于N.
(1)如图1,当D,B,F共线时,求证:
①EB=EP;
②∠EFP=30°;
(2)如图2,当D,B,F不共线时,连接BF,求证:∠BFD+∠EFP=30°.
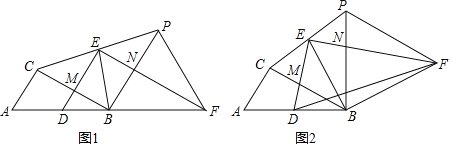
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书已知甲图书每本价格是乙图书每本价格的![]() 倍,用
倍,用![]() 元单独购买甲图书比用
元单独购买甲图书比用![]() 元单独购买乙图书要少
元单独购买乙图书要少![]() 本.
本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的![]() 倍少
倍少![]() 本,且用于购买甲、乙两种图书的总经费不超过
本,且用于购买甲、乙两种图书的总经费不超过![]() 元,那么该图书馆最多可以购买多少本乙图书?
元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() 、
、![]() ;③若直线
;③若直线![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() 两点则
两点则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系是
的大小关系是![]() ;④当
;④当![]() 时,
时,![]() ;⑤
;⑤![]() ,
,
其中正确的说法有( )
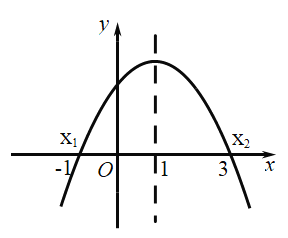
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com