【题目】二次函数
的图象如图所示，给出下列说法：
①
；②方程
的根为
、
；③若直线
与的图象相交于
，
，
两点则
、
、
、
的大小关系是
；④当
时，
；⑤
，
其中正确的说法有（ ）
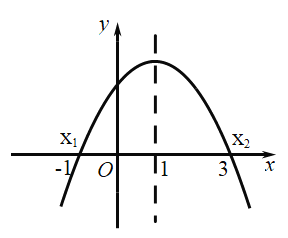
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据抛物线的开口方向、对称轴和与y轴的交点即可判断a、b、c的符号，从而判断①；然后根据抛物线与x轴的交点坐标即可判断②；根据题意，画出直线y=2，即可判断③；根据图象即可判断④；将对称轴和（-1,0）代入即可得出a、b、c的关系，从而判断⑤．
解：由抛物线的开口向下，对称轴为直线x=1，与y轴的交点在正半轴上
∴a＜0，b＞0，c＞0
∴
，故①正确；
由图象可知：抛物线与x轴的交点坐标为（-1,0）、（3,0）
∴方程
的根为
、
，故②正确；
如下图所示，画出直线y=2
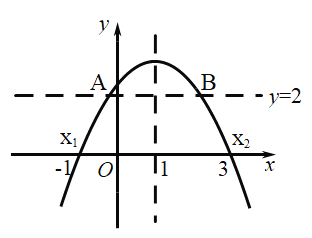
由图可知：
，故③错误；
由图象可知：当
时，
，故④正确；
∵由抛物线的对称轴可知：
，
∴b=-2a
将（-1,0）代入到解析式中，得
a－b＋c=0
∴a－（-2a）＋c=0
解得：c=-3a
∴
=
=
∵a＜0
∴＞0
∴＞0，故⑤正确．
综上：正确的结论有4个
故选D．
浙江名校名师金卷系列答案科目：初中数学 来源： 题型：
【题目】如图，两个全等的等腰直角三角形放置在平面直角坐标系中，
在
轴上，
，
，反比例函数
的图象经过点
．
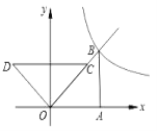
（1）求反比例函数的解析式；
（2）把
沿射线
移动，当点
落在图象上的
时，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，为了测量建筑物CD、EF的高度，在直线CE上选取观测点A、B，AC的距离为40米．从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°，从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°．
（1）求建筑物CD的高度；
（2）求建筑物EF的高度．
（参考数据：tan51.34°≈1.25，tan68.20°≈2.5，tan64.43°≈2，tan26.57°≈0.5）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，甲出发1h后，乙出发，设甲与A地相距y甲（km），乙与A地相距y乙（km），甲离开A地的时间为x（h），y甲，y乙与x之间的函数图象如图所示．
（1）甲的速度是 km/h；
（2）当1≤x≤5时，求y乙关于x的函数关系式；
（3）当乙与A地相距240km时，直接写出甲与A地的距离．
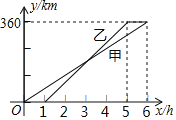
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】网络销售是一种重要的销售方式．某乡镇农贸公司新开设了一家网店，销售当地农产品．其中一种当地特产在网上试销售，其成本为每千克10元．公司在试销售期间，调查发现，每天销售量y（kg）与销售单价x（元）满足如图所示的函数关系（其中
）．
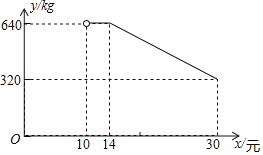
（1）直接写出y与x之间的函数关系式及自变量的取值范围．
（2）若农贸公司每天销售该特产的利润要达到3100元，则销售单价x应定为多少元？
（3）设每天销售该特产的利润为W元，若
，求：销售单价x为多少元时，每天的销售利润最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学习网站针对疫情停课不停学推出了套餐优惠服务：已知购买2个学习账号和1个错题伴印设备需要2700元，购买3个学习账号和2个错题伴印设备需要4800元．
（1）求1个学习账号和1个错题伴印设备的单价各是多少元？
（2）若某学习小组准备购买账号和错题伴印设备共45个，且要求伴印设备不低于账号数量的
，请问如何购买才能使得总费用最低，最低费用为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
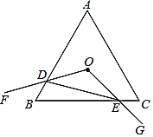
【题目】如图，等边三角形
的边长为8，点
是
的内心，
，绕点旋转
，分别交线段
、
于
、
两点，连接
，给出下列四个结论：①点也一定是的外心；②
；③四边形
的面积始终等于
；④
周长的最小值为6．上述结论中正确的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
