
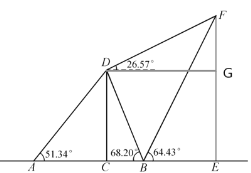
【题目】如图,为了测量建筑物CD、EF的高度,在直线CE上选取观测点A、B,AC的距离为40米.从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°,从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°.
(1)求建筑物CD的高度;
(2)求建筑物EF的高度.
(参考数据:tan51.34°≈1.25,tan68.20°≈2.5,tan64.43°≈2,tan26.57°≈0.5)

【答案】(1)建筑物CD的高度为50米;(2)建筑物EF的高度为80米.
【解析】
(1)在Rt△ACD中,∠ACD=90°,tan∠DAC=![]() ,即可得到结果;
,即可得到结果;
(2)过点D作DG⊥EF于点G ,证明四边形DCEG是矩形,得到CD=EG=50,DG=CE,根据Rt△DFG可求出DG,根据Rt△FBE求出BE,即可得到结果.
解:(1)在Rt△ACD中,∠ACD=90°,
∵tan∠DAC=![]() ,
,
∴CD=AC·tan51.34°≈40×1.25=50.
(2)过点D作DG⊥EF于点G.
在Rt△BCD中,∠BCD=90°,
∵tan∠DBC=![]() ,
,
∴BC=![]() .
.
根据![]() ,
,![]() ,
,![]() ,可得四边形DCEG是矩形,
,可得四边形DCEG是矩形,
∴CD=EG=50,DG=CE.
设EF=x米.
在Rt△DFG中,∠DGF=90°,
∵tan∠FDG=![]() ,
,
∴DG=![]() ,
,
在Rt△FBE中,∠BEF=90°,
∵tan∠FBE=![]() ,
,
∴BE=![]() ,
,
∴![]() =20+
=20+![]() ,
,
∴x≈80.
答:建筑物CD的高度为50米,建筑物EF的高度为80米.


科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书已知甲图书每本价格是乙图书每本价格的![]() 倍,用
倍,用![]() 元单独购买甲图书比用
元单独购买甲图书比用![]() 元单独购买乙图书要少
元单独购买乙图书要少![]() 本.
本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的![]() 倍少
倍少![]() 本,且用于购买甲、乙两种图书的总经费不超过
本,且用于购买甲、乙两种图书的总经费不超过![]() 元,那么该图书馆最多可以购买多少本乙图书?
元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ、PB、QC是⊙O的切线,切点分别为A、B、C,点D在![]() 上,若∠D=100°,则∠P与∠Q的度数之和是( )
上,若∠D=100°,则∠P与∠Q的度数之和是( )
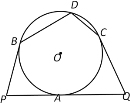
A.160°B.140°C.120°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
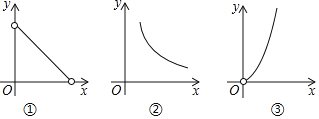
【题目】在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个数学问题:
问题a:矩形面积为4,它的长y与宽x之间的函数关系;
问题b:矩形周长为8,它的长y与宽x之间的函数关系.
(1)问题a,b所对应的函数图象分别为 ,(填写序号);
(2)请你把剩下的函数图象写出一个适合的数学问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() 、
、![]() ;③若直线
;③若直线![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() 两点则
两点则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系是
的大小关系是![]() ;④当
;④当![]() 时,
时,![]() ;⑤
;⑤![]() ,
,
其中正确的说法有( )
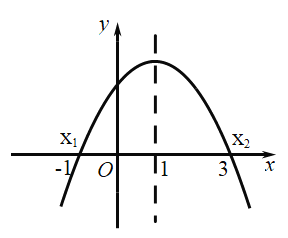
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
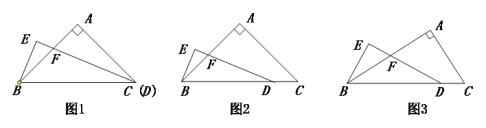
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com