练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

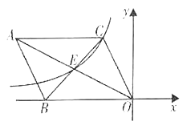
    【题目】如图，在中，对角线，交于点，双曲线经过，两点若的面积为，则的值是（ ）

    A.B.C.D.

    【答案】B

    【解析】

    设E的坐标是（m，n），则mn=k，平行四边形ABOC中E是OA的中点，则A的坐标是：（2m，2n），C的纵坐标是2n，表示出C的横坐标，则可以得到AC即OB的长，然后根据平行四边形的面积公式即可求得k的值．

    解：设E的坐标是（m，n），则mn=k，
    ∵平行四边形ABOC中E是OA的中点，
    ∴A的坐标是：（2m，2n），C的纵坐标是2n，
    把y=2n代入 得：x=，即C的横坐标是：．
    ∴OB=AC=-2m，OB边上的高是2n，
    ∴（，-2m）2n=10，
    即k-4mn=10，
    ∴k-4k=10，
    解得：k=- ．
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，等边三角形的顶点，分别在反比例函数图象的两个分支上，点在反比例函数的图象上，轴．当的面积最小时，的值为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

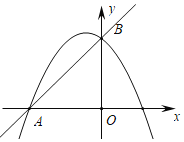
    【题目】在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过点、．

    (1)求、满足的关系式及的值．

    (2)当时，若的函数值随的增大而增大，求的取值范围．

    (3)如图，当时，在抛物线上是否存在点，使的面积为1？若存在，请求出符合条件的所有点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

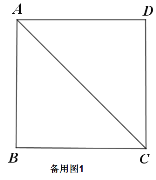
    【题目】如图（1），已知点在正方形的对角线上，垂足为点，垂足为点．

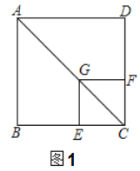
    （1）证明与推断：

    求证：四边形是正方形；

    推断：的值为_ _；

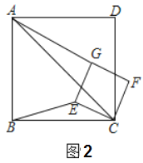
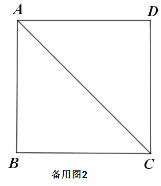
    （2）探究与证明：

    将正方形绕点顺时针方向旋转角，如图（2）所示，试探究线段与之间的数量关系，并说明理由；

    （3）拓展与运用：

    若，正方形在绕点旋转过程中，当三点在一条直线上时，则 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点为坐标原点．抛物线交轴于、两点，交轴于点，直线经过、两点．

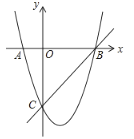
    （1）求抛物线的解析式；

    （2）过点作直线轴交抛物线于另一点，过点作轴于点，连接，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

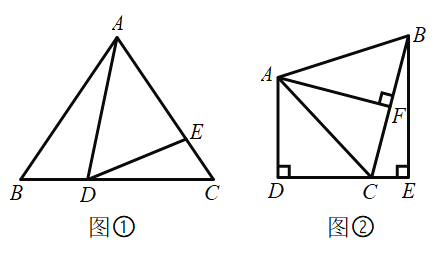
    【题目】如图①，在中，，点，分别是边，上的点，且．

    （1）若，，设，，求关于的函数关系式；

    （2）如图②，，于点，于点，于点，点在线段上，，，，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两个全等的等腰直角三角形放置在平面直角坐标系中，在轴上，，，反比例函数的图象经过点．

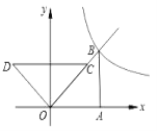
    （1）求反比例函数的解析式；

    （2）把沿射线移动，当点落在图象上的时，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查，并将得到的数据整理成了以下统计图（不完整）．

    （1）此次共调查了 名学生；

    （2）请将条形统计图补充完整；

    （3）若该学校九年级共有300名学生，请你估计其中“非常喜欢”网课的人数．

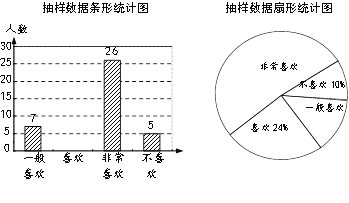
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为了测量建筑物CD、EF的高度，在直线CE上选取观测点A、B，AC的距离为40米．从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°，从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°．

    （1）求建筑物CD的高度；

    （2）求建筑物EF的高度．

    （参考数据：tan51.34°≈1.25，tan68.20°≈2.5，tan64.43°≈2，tan26.57°≈0.5）

    查看答案和解析>>

    同步练习册答案