
【题目】如图①,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() .
.
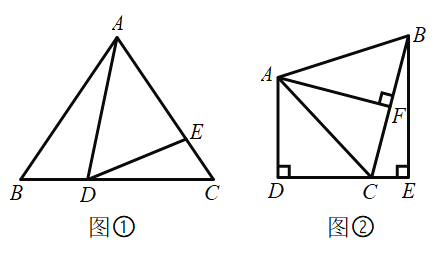
(1)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如图②,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先证明△ABD∽△DCE,进而可得ABCE=BDCD,由此可得![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)先利用等腰三角形的三线合一证得AF⊥BC,BF =5,再利用勾股定理计算即可求得答案.
(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADC为△ABD的外角,
∴∠ADC=∠ADE+∠EDC=∠B+∠DAB.
∵∠ADE=∠B,
∴∠BAD=∠CDE.
又∠B=∠C,
∴△ABD∽△DCE.
∴![]() ,
,
∴ABCE=BDCD,
则5×(5-y)=x(6-x),
整理,得![]() .
.
(2)解:∵AB=AC,AF⊥BC,
∴BF=CF=![]() BC=5.
BC=5.
∴在Rt△ACF中,AC=![]() .
.
∴在Rt△ACD中,DC=![]() .
.
在Rt△BCE中,CE=![]() .
.
∴DE=DC+CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】抗击疫情,人人有责,某校成立教师志愿者分队,共分宣传、测温、清理(主要厨余垃圾清理)、统计(师生疫情信息统计)四组,为了解教师对这四个小组的参与意愿情况调查,对教师进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表.
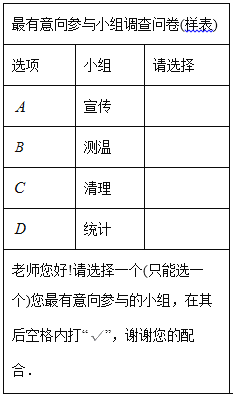
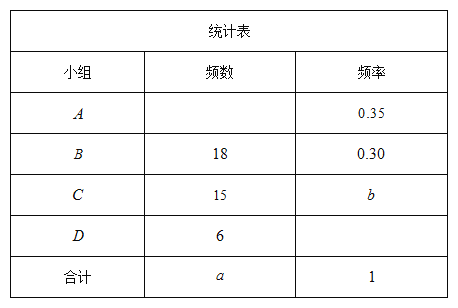
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _ ,b=_ ;
_ ,b=_ ;
(2)根据调查结果,请你估计该市![]() 名教师中最有意向参与清理小组的人数;
名教师中最有意向参与清理小组的人数;
(3)王老师和李老师选择参与小组,若他们每人从![]() 四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店3月份购进甲种水果50千克、乙种水果80千克,共花费1700元,其中甲种水果以15元/千克,乙种水果以20元/千克全部售出;4月份又以同样的价格购进甲种水果60千克、乙种水果40千克,共花费1200元,由于市场不景气,4月份两种水果均以3月份售价的8折全部售出.
(1)求甲、乙两种水果的进价每千克分别是多少元?
(2)请计算该水果店3月和4月甲、乙两种水果总赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级学生在寒假期间积极抗击疫情,开展老师“在你身边”评星活动,学生可以从“自理星” 、“读书星”、“健康星”、“孝敬星”、“ 劳动星”等中选一个项目参加争星竞选,根据该校八年级学生的“争星”报名情况,绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
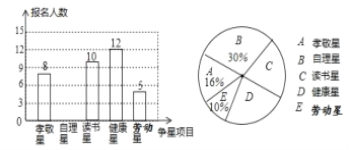
(1)参加年级评星的学生共有________人;将条形统计图补充完整;
(2)扇形统计图中“读书星”对应的扇形圆心角度数是________;
(3)若八年级1班准备推荐甲、乙、丙、丁四名同学中的2名代表班级参加学校的“劳动星” 报名,请用表格或树状图分析甲和乙同学同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3﹣(n2+1)x+n=x3﹣n2x﹣x+n=x(x2﹣n2)﹣(x﹣n)=x(x﹣n)(x+n)﹣(x﹣n)=(x﹣n)(x2+nx﹣1).
理解运用:如果x3﹣(n2+1)x+n=0,那么(x﹣n)(x2+nx﹣1)=0,即有x﹣n=0或x2+nx﹣1=0,
因此,方程x﹣n=0和x2+nx﹣1=0的所有解就是方程x3﹣(n2+1)x+n=0的解.
解决问题:求方程x3﹣5x+2=0的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数
与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数![]() (
(![]() )的图像为直线
)的图像为直线![]() .
.
(1)求A、B两点的坐标;
(2)当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]() ,试说明:抛物线G的顶点不在直线
,试说明:抛物线G的顶点不在直线![]() 上;
上;
(3)设![]() ,直线
,直线![]() 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线
与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线![]() 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
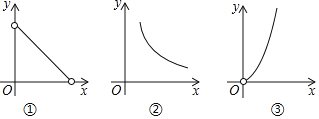
【题目】在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个数学问题:
问题a:矩形面积为4,它的长y与宽x之间的函数关系;
问题b:矩形周长为8,它的长y与宽x之间的函数关系.
(1)问题a,b所对应的函数图象分别为 ,(填写序号);
(2)请你把剩下的函数图象写出一个适合的数学问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com