
����Ŀ��ijˮ����3�·ݹ�������ˮ��50ǧ�ˡ�����ˮ��80ǧ�ˣ�������1700Ԫ�����м���ˮ����15Ԫ/ǧ�ˣ�����ˮ����20Ԫ/ǧ��ȫ���۳���4�·�����ͬ���ļ۸�����ˮ��60ǧ�ˡ�����ˮ��40ǧ�ˣ�������1200Ԫ�������г���������4�·�����ˮ������3�·��ۼ۵�8��ȫ���۳���
��1����ס�������ˮ���Ľ���ÿǧ�˷ֱ��Ƕ���Ԫ��
��2��������ˮ����3�º�4�¼ס�������ˮ����Ӯ������Ԫ��
���𰸡���1������ˮ���Ľ���Ϊÿǧ��10Ԫ������ˮ���Ľ���Ϊÿǧ��15Ԫ����2�� 810Ԫ��
��������
��1�������ˮ���Ľ���Ϊÿǧ��xԪ������ˮ���Ľ���Ϊÿǧ��yԪ����������������ˮ��50ǧ�ˡ�����ˮ��80ǧ�ˣ�������1700Ԫ����������ˮ��60ǧ�ˡ�����ˮ��40ǧ�ˣ�������1200Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2������������ÿǧ���������������������������ˮ����3�º�4�����ۼס�������ˮ������Ӯ����
�⣺��1�������ˮ���Ľ���Ϊÿǧ��xԪ������ˮ���Ľ���Ϊÿǧ��yԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺼���ˮ���Ľ���Ϊÿǧ��10Ԫ������ˮ���Ľ���Ϊÿǧ��15Ԫ��
��2��50����15��10��+80����20��15��+60����15��0.8��10��+40����20��0.8��15����810��Ԫ����
�𣺸�ˮ����3�º�4�¼ס�������ˮ����Ӯ��810Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪������y=x2-1��x�ύ��A��B���㣬��y�ύ�ڵ�C��
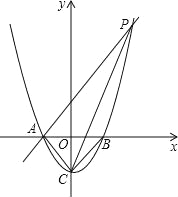
��1����A��B��C��������ꣻ
��2������A��AP��CB���������ڵ�P�����ı���ACBP�������
��3����x���Ϸ������������Ƿ����һ��M����M��MG��x���ڵ�G��ʹ��A��M��G����Ϊ��������������PCA���ƣ������ڣ������M������ꣻ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ������������![]() ���ּ���Ʒ����160Ԫ������
���ּ���Ʒ����160Ԫ������![]() �ּ���Ʒ����240Ԫ������
�ּ���Ʒ����240Ԫ������![]() �ּ���Ʒ��������ͬ��ÿ��
�ּ���Ʒ��������ͬ��ÿ��![]() �ּ���Ʒ�Ľ��۱�
�ּ���Ʒ�Ľ��۱�![]() �ּ���Ʒ�Ľ��۹�10Ԫ��
�ּ���Ʒ�Ľ��۹�10Ԫ��
��1����![]() ���ּ���Ʒÿ���Ľ��۷ֱ�Ϊ����Ԫ��
���ּ���Ʒÿ���Ľ��۷ֱ�Ϊ����Ԫ��
��2�������̵�![]() �ּ���Ʒÿ���ۼ�24Ԫ��
�ּ���Ʒÿ���ۼ�24Ԫ��![]() �ּ���Ʒÿ���ۼ�35Ԫ�������ּ���Ʒ������1000���������ּ���Ʒȫ���۳����ܻ���������4900Ԫ����
�ּ���Ʒÿ���ۼ�35Ԫ�������ּ���Ʒ������1000���������ּ���Ʒȫ���۳����ܻ���������4900Ԫ����![]() �ּ���Ʒ�������ټ���
�ּ���Ʒ�������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С����5����Ա�����ߣ���λ��cm���ֱ�Ϊ��160��165��170��163��172��������160 cm�ij�Ա�滻��һλ165 cm�ij�Ա���ֿ���С���Ա��������ԭ����ȣ�����˵����ȷ���ǣ� ��
A.ƽ������С�������СB.ƽ�����������
C.ƽ����������D.ƽ����������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
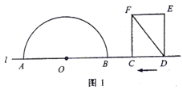
����Ŀ����ͼ1,��![]() �;���
�;���![]() �ı�
�ı�![]() ����ֱ��
����ֱ��![]() ��,�Ե�
��,�Ե�![]() ΪԲ��,��24Ϊ�뾶����Բ,�ֱ�ֱ��
ΪԲ��,��24Ϊ�뾶����Բ,�ֱ�ֱ��![]() ��
��![]() ����.��֪:
����.��֪: ![]() ,
,![]() ,��������������ֱ��
,��������������ֱ��![]() ��ƽ��,����
��ƽ��,����![]() �����
�����![]() ʱ,����ֹͣ�˶�.��ƽ�ƹ�����,����ζԽ���
ʱ,����ֹͣ�˶�.��ƽ�ƹ�����,����ζԽ���![]() ���Բ
���Բ![]() �Ľ���Ϊ
�Ľ���Ϊ![]() (��
(��![]() Ϊ��Բ��Զ���
Ϊ��Բ��Զ���![]() �Ľ���).
�Ľ���).
��1����ͼ2����![]() ���Բ
���Բ![]() ���У���
���У���![]() ��ֵ��
��ֵ��
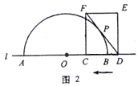
��2����ͼ3����![]() ���Բ
���Բ![]() ����������ʱ�����߶�
����������ʱ�����߶�![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�����߶�![]() �ij�Ϊ20��ֱ��д����ʱ
�ij�Ϊ20��ֱ��д����ʱ![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
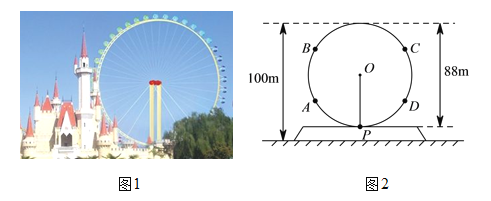
����Ŀ��ij������Ħ����(��ͼ1)�о��ȷֲ���Բ��ת�ֱ�Ե�����ɸ����գ��������������п��Ը��������ͼ2��Ħ���ֵ�ʾ��ͼ��Ħ�����Թ̶����ٶ�������![]() ˳ʱ�뷽��ת����תһȦΪ
˳ʱ�뷽��ת����תһȦΪ![]() ���ӣ���С���ɵDzյ�
���ӣ���С���ɵDzյ�![]() ����Ħ���ֿ�ʼ��ʱ������12����ʱ�������������յ���ͼ2�еĵ�_________��(��
����Ħ���ֿ�ʼ��ʱ������12����ʱ�������������յ���ͼ2�еĵ�_________��(��![]() ��
��![]() ��
��![]() ��
��![]() )���˵�����ĸ߶�Ϊ_______m��
)���˵�����ĸ߶�Ϊ_______m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������̫�����������ź��ǣ�������̫��ϵ�����һ�ź��dz�Ϊ�������ǡ���������̫��ϵԼ4.2����.����������ѧ��һ�ּ�������ʱ�վ���ij��ȵ�λ��1����ԼΪ9500000000000ǧ��.�����ǡ�����̫��ϵԼΪ�� ��
A. ![]() ǧ��B.
ǧ��B. ![]() ǧ��C.
ǧ��C. ![]() ǧ��D.
ǧ��D. ![]() ǧ��
ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
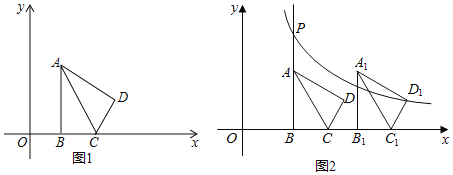
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У���֪��ABC����ABC=90��������A�ڵ�һ���ޣ�B��C��x����������ϣ�C��B���Ҳࣩ��BC=2��AB=2![]() ����ADC����ABC����AC���ڵ�ֱ�߶Գƣ�
����ADC����ABC����AC���ڵ�ֱ�߶Գƣ�
��1����OB=2ʱ�����D�����ꣻ
��2������A�͵�D��ͬһ��������������ͼ���ϣ���OB�ij���
��3����ͼ2�����ڣ�2�����е��ı���ABCD����ƽ�ƣ���ƽ�ƺ���ı���ΪA1B1C1D1������D1�ķ���������y=![]() ��k��0����ͼ����BA���ӳ��߽��ڵ�P���ʣ���ƽ�ƹ����У��Ƿ����������k��ʹ���Ե�P��A1��DΪ�������������ֱ�������Σ������ڣ���ֱ��д�����з��������k��ֵ���������ڣ���˵�����ɣ�
��k��0����ͼ����BA���ӳ��߽��ڵ�P���ʣ���ƽ�ƹ����У��Ƿ����������k��ʹ���Ե�P��A1��DΪ�������������ֱ�������Σ������ڣ���ֱ��д�����з��������k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
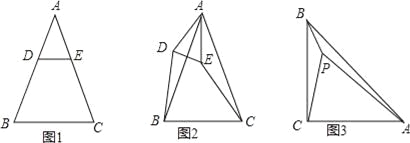
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DB EC������������������������=����
��2������̽��������ͼ1�е���ADE�Ƶ�A˳ʱ����ת����0��������180������ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90������PB=1��PC=2��PA=3������BPC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com