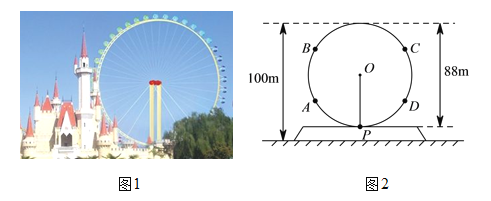
【题目】某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱，人们坐在座舱中可以俯瞰美景，图2是摩天轮的示意图．摩天轮以固定的速度绕中心
顺时针方向转动，转一圈为
分钟．从小刚由登舱点
进入摩天轮开始计时，到第12分钟时，他乘坐的座舱到达图2中的点_________处(填
，
，
或
)，此点距地面的高度为_______m．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+80．设这种产品每天的销售利润为w元．
（1）求w与x之间的函数关系式．
（2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AD=
AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，其中正确的有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
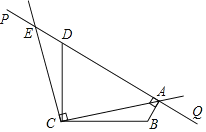
【题目】如图，∠BCD＝90°，且BC＝DC，直线PQ经过点D．设∠PDC＝α（45°＜α＜135°），BA⊥PQ于点A，将射线CA绕点C按逆时针方向旋转90°，与直线PQ交于点E．
（1）当α＝125°时，∠ABC＝ °；
（2）求证：AC＝CE；
（3）若△ABC的外心在其内部，直接写出α的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果店3月份购进甲种水果50千克、乙种水果80千克，共花费1700元，其中甲种水果以15元/千克，乙种水果以20元/千克全部售出；4月份又以同样的价格购进甲种水果60千克、乙种水果40千克，共花费1200元，由于市场不景气，4月份两种水果均以3月份售价的8折全部售出．
（1）求甲、乙两种水果的进价每千克分别是多少元？
（2）请计算该水果店3月和4月甲、乙两种水果总赢利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，抛物线
：
沿
轴翻折得到抛物线
.
（1）求抛物线的顶点坐标；
（2）横、纵坐标都是整数的点叫做整点．
① 当
时，求抛物线和围成的封闭区域内(包括边界)整点的个数；
② 如果抛物线C1和C2围成的封闭区域内(包括边界)恰有
个整点，求m取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
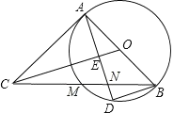
【题目】如图，AB是⊙O的直径，CA与⊙O相切于点A，且CA＝BA．连接OC，过点A作AD⊥OC于点E，交⊙O于点D，连接DB．
（1）求证：△ACE≌△BAD；
（2）连接CB交⊙O于点M，交AD于点N．若AD＝4，求MN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在ABCD中，DE平分∠ADB，交AB于E，BF平分∠CBD，交CD于F．
（1）求证：△ADE≌△CBF；
（2）当AD与BD满足什么关系时，四边形DEBF是矩形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了加快“智慧校园”建设，某市准备为试点学校采购一批
、
两种型号的一体机，经过市场调查发现，今年每套型一体机的价格比每套型一体机的价格多0.6万元，且用960万元恰好能购买500套型一体机和200套型一体机.
（1）求今年每套型、型一体机的价格各是多少万元
（2）该市明年计划采购型、型一体机1100套，考虑物价因素，预计明年每套型一体机的价格比今年上涨25%，每套型一体机的价格不变，若购买型一体机的总费用不低于购买型一体机的总费用，那么该市明年至少需要投入多少万元才能完成采购计划？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
