
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
试题∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AE=AD,
又∠ABE=∠AHD=90°
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵∠AHB=![]() (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=∠AED,
∴OE=OH,
∵∠DOH=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DOH=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
又BE=DH,∠AEB=∠HDF=45°
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
由上述①、②、③可得CD=BE、DF=EH=CE,CF=CD-DF,
∴BC-CF=(CD+HE)-(CD-HE)=2HE,所以④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故选C.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
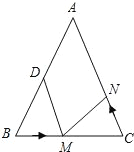
【题目】如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为_____厘米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销售量y(件)与零售价x(元/件)均成一次函数关系.(如图) 
(1)求y与x的函数关系式;
(2)该店计划这次选购A、B两种文具的数量共100件,所花资金不超过1000元,并希望全部售完获利不低于296元,若按A种文具每件可获利4元和B种文具每件可获利2元计算,则该店这次有哪几种进货方案?
(3)若A种文具的零售价比B种文具的零售价高2元/件,求两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间的函数关系式,并说明A、B两种文具零售价分别为多少时,每天销售的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,

(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com