
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
【答案】解:(1)由题意得:![]() ,
,
∴w与x的函数关系式为:![]() 。
。
(2)![]() ,
,
∵﹣2<0,∴当x=30时,w有最大值.w最大值为200。
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元。
(3)当w=150时,可得方程﹣2(x﹣30)2+200=150,解得x1=25,x2=35。
∵35>28,∴x2=35不符合题意,应舍去。
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元。
【解析】
试题(1)根据销售额=销售量×销售价单x,列出函数关系式。
(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值。
(3)把y=150代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值。


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(﹣1,0),请按要求画图与作答.

(1)把△ABC绕点P旋转180°得△A′B′C′.
(2)把△ABC向右平移7个单位得△A″B″C″.
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′,并写出其坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是

A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于![]() AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.

(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点0,AC=2,BD=![]() .将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )
.将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°
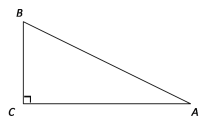
(1)尺规作图:作AC的垂直平分线,垂足为E,交AB于点D.(不写作法,保留作图痕迹,不证明)
(2)连结CD,求证: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com