
【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于![]() AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.

(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
【答案】(1)证明见解析;(2)四边形ACDB的面积为8![]() .
.
【解析】
(1)依题可得:AC=CD,AB=DB,BC是∠FCE的角平分线,根据角平分线的定义和平行线的性质得∠ACB=∠ABC,根据等角对等边得AC=AB,从而得AC=CD=DB=BA,根据四边相等得四边形是菱形即可得四边形ACDB是菱形;再根据题中的新定义即可得证.
(2)设菱形ACDB的边长为x,根据已知可得CF=6,CE=12,FA=6-x,根据相似三角形的判定和性质可得 ![]() ,解得:x=4,过点A作AH⊥CD于点H,在Rt△ACH中,根据锐角三角形函数正弦的定义即可求得AH ,再由四边形的面积公式即可得答案.
,解得:x=4,过点A作AH⊥CD于点H,在Rt△ACH中,根据锐角三角形函数正弦的定义即可求得AH ,再由四边形的面积公式即可得答案.
(1)由已知得:AC=CD,AB=DB,由已知尺规作图痕迹得:BC是∠FCE的角平分线,
∴∠ACB=∠DCB,
又∵AB∥CD,
∴∠ABC=∠DCB,
∴∠ACB=∠ABC,
∴AC=AB,
又∵AC=CD,AB=DB,
∴AC=CD=DB=BA,
![]() 四边形ACDB是菱形,
四边形ACDB是菱形,
又∵∠ACD与△FCE中的∠FCE重合,它的对角∠ABD顶点在EF上,
∴四边形ACDB为△FEC的亲密菱形.
(2)设菱形ACDB的边长为x,∵CF=6,CE=12,
∴FA=6-x,
又∵AB∥CE,
∴△FAB∽△FCE,
∴ ![]() ,
,
即 ![]() ,
,
解得:x=4,
过点A作AH⊥CD于点H,
在Rt△ACH中,∠ACH=45°,
∴sin∠ACH= ![]() ,
,
∴AH=4× ![]() =2
=2![]() ,
,
∴四边形ACDB的面积为: ![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
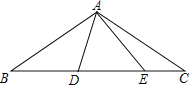
【题目】如图,在△ABC中,AB=AC=2![]() ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
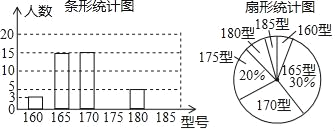
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如下两个不完整的统计图(校服型号以身高作为标准,共分为6种型号)
根据以上信息,解答下列问题:
(1)该班共有 名学生.
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,185型校服所对应扇形圆心角=
(4)若全校九年级共有学生800名,请估计穿170型校服的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
查看答案和解析>>
科目:初中数学 来源: 题型:
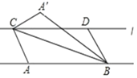
【题目】如图,已知直线![]() ∥AB,
∥AB,![]() 与 AB 之间的距离为 2 ,C、D 是直线
与 AB 之间的距离为 2 ,C、D 是直线![]() 上
上![]() 两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:2x2﹣7x+6=0;
(2)已知:关于x的方程x2+kx﹣2=0.
①求证:方程有两个不相等的实数根;
②若方程的一个根是﹣1,求另一个根及k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
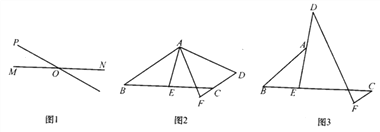
【题目】(l)操作:如图1,点O为线段MN的中点,直线PQ与MN相交于点O,请利用图1画出一对以点O为对称中心的全等三角形;根据上述操作得到的经验完成下列探究活动:
(2)探究一:如图2,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.试探究线段AB与AF,AF,CF之间的等量关系,并证明你的结论;
(3)探究二:如图3 ,DE,BC相交于点E,BA交DE于点A,且BE:EC=1:2,∠BAE=∠EDF,CF∥AB.若AB=5,CF=1,求DF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com