
【题目】(1)解方程:2x2﹣7x+6=0;
(2)已知:关于x的方程x2+kx﹣2=0.
①求证:方程有两个不相等的实数根;
②若方程的一个根是﹣1,求另一个根及k值.
【答案】(1)x1=2,x2= ![]() ;(2)①答案见解析;(2)k的值为﹣1,方程另一根为2.
;(2)①答案见解析;(2)k的值为﹣1,方程另一根为2.
【解析】试题分析:(1)利用求根公式进行求解即可得;
(2)①利用根据的判别式进行证明即可;
②先求出k的值,然后再解方程即可得.
试题解析:(1)∵2x2﹣7x+6=0,
∴a=2,b=﹣7,c=6,
∴△=(﹣7)2﹣4×2×6=1,
∴x=![]() ,
,
∴x1=2,x2= ![]() ;
;
(2)①∵x2+kx﹣2=0,
∴△=k2﹣4×(﹣2)=k2+8>0,
∴方程有两个不相等的实数根;
②∵方程的一个根是﹣1,
∴1﹣k﹣2=0,解得k=﹣1,
∴方程为x2﹣x﹣2=0,解得x=﹣1或x=2,
即k的值为﹣1,方程另一根为2.


科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于![]() AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.

(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学公益组织计划购买![]() 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元.
套装共需820元.
(1)求购买一套![]() 套装文具、一套
套装文具、一套![]() 套装各需要多少元?
套装各需要多少元?
(2)根据该公益组织的募捐情况和捐助对象情况,需购买![]() 两种套装共60套,要求购买
两种套装共60套,要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多多少套?
套装最多多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线![]() (k≠0)与
(k≠0)与![]() 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
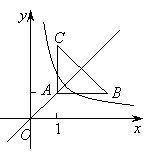
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在AB、AC上,BE与CD相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABE≌△ACD( )

A. AD=AEB. AB=AC
C. BE=CDD. ∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com