
【题目】某大学公益组织计划购买![]() 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元.
套装共需820元.
(1)求购买一套![]() 套装文具、一套
套装文具、一套![]() 套装各需要多少元?
套装各需要多少元?
(2)根据该公益组织的募捐情况和捐助对象情况,需购买![]() 两种套装共60套,要求购买
两种套装共60套,要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多多少套?
套装最多多少套?
【答案】(1)购买一套![]() 套装需要100元,购买一套
套装需要100元,购买一套![]() 套装需要80元;(2)购买
套装需要80元;(2)购买![]() 套装最多22套.
套装最多22套.
【解析】
(1)设购买一套![]() 套装需要
套装需要![]() 元,购买一套
元,购买一套![]() 套装凳需要
套装凳需要![]() 元,根据“买
元,根据“买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元”,即可得出关于
套装共需820元”,即可得出关于![]() 的二元一次方程组,解之即可得出结论;
的二元一次方程组,解之即可得出结论;
(2)设购买![]() 套装
套装![]() 套,则购买
套,则购买![]() 套装
套装![]() 套,根据购买
套,根据购买![]() 两种套装的总费用不超过5240元列不等式即可得到结论.
两种套装的总费用不超过5240元列不等式即可得到结论.
解:(1)设购买一套![]() 套装需要
套装需要![]() 元,购买一套
元,购买一套![]() 套装凳需要
套装凳需要![]() 元,
元,
根据题意得:![]() ,
,
解得:![]() .
.
答:购买一套![]() 套装需要100元,购买一套
套装需要100元,购买一套![]() 套装需要80元;
套装需要80元;
(2)设购买![]() 套装
套装![]() 套,则购买
套,则购买![]() 套装
套装![]() 套,根据题意得
套,根据题意得![]() ,
,
解得:![]() ,
,
∴购买![]() 套装最多22套,
套装最多22套,
答:要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多22套.
套装最多22套.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
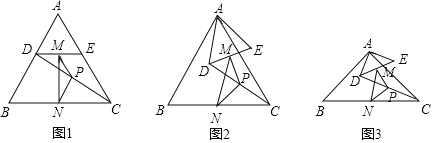
【题目】如图,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
在如图中,线段PM与PN的数量关系是______,∠MPN的度数是______;
(2)探究证明
把△ADE绕点A逆时针方向旋转到如图的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸
若△ABC为直角三角形,∠BAC=90°,AB=AC=12,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图.
①△PMN的是______三角形.
②直接利用①中的结论,求△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
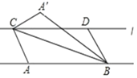
【题目】如图,已知直线![]() ∥AB,
∥AB,![]() 与 AB 之间的距离为 2 ,C、D 是直线
与 AB 之间的距离为 2 ,C、D 是直线![]() 上
上![]() 两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
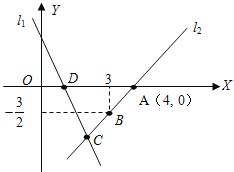
【题目】如图,直线![]() 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
(1)求点D的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线![]() 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:2x2﹣7x+6=0;
(2)已知:关于x的方程x2+kx﹣2=0.
①求证:方程有两个不相等的实数根;
②若方程的一个根是﹣1,求另一个根及k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )

A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
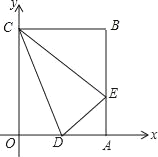
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com