
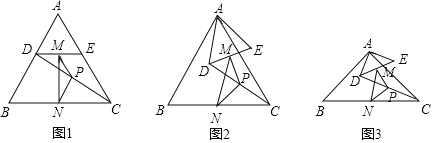
【题目】如图,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
在如图中,线段PM与PN的数量关系是______,∠MPN的度数是______;
(2)探究证明
把△ADE绕点A逆时针方向旋转到如图的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸
若△ABC为直角三角形,∠BAC=90°,AB=AC=12,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图.
①△PMN的是______三角形.
②直接利用①中的结论,求△PMN面积的最大值.
【答案】(1)PM=PN,120°.(2)①△PMN是等腰三角形.证明见解析;②120°.(3)①等腰直角;②32.
【解析】
(1)结论:PM=PN,120°.利用三角形的中位线定理即可解决问题;
(2)①如图2中,连接BD、EC.证明△BAD≌△CAE(SAS),可得BD=EC,再利用三角形中位线定理即可解决问题;
②利用三角形的外角以及平行线的性质即可解决问题;
(3)①由(2)可知:△PMN是等腰直角三角形;
②因为PM=PN=![]() BD,推出BD最大时,PM最大,△PMN面积最大.
BD,推出BD最大时,PM最大,△PMN面积最大.
(1)结论:PM=PN,120°.
理由:如图1中,∵△ABC是等边三角形,
∴AB=AC,
∵AD=AE,
∴BD=EC,
∵点M,P,N分别为DE,DC,BC的中点,
∴PM=![]() EC,PN=
EC,PN=![]() BD,PM∥AC,PN∥AB,
BD,PM∥AC,PN∥AB,
∴PM=PN,∠MPD=∠ACD,∠PNC=∠B=60°,
∵∠MPN=∠MPD+∠DPN=∠ACD+∠DCB+∠PNC=120°,
故答案为PM=PN,120°;
(2)如图2中,连接BD、EC,
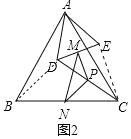
①∵∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
∵BA=CA,DA=EA,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵点M,P,N分别为DE,DC,BC的中点,
∴PN∥BD,PM∥EC,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PN=PM,
∴△PMN是等腰三角形;
②∵PN∥BD,PM∥EC,
∴∠PNC=∠DBC,∠DPM=∠A=ECD,
∴∠MPN=∠MPD+∠DPN=∠ECD+∠PNC+∠DCB=∠ECD+∠DCB+∠DBC=∠ACE+∠ACD+∠DCB+∠DBC=∠ABD+∠ACB+∠DBC=∠ACB+∠ABC=120°;
(3)①△PMN是等腰直角三角形;
②∵PM=PN=![]() BD,
BD,
∴BD最大时,PM最大,△PMN面积最大,
∴点D在BA的延长线上,
∴BD=AB+AD=16,∴PM=8,∴S△PMN最大=![]() PM2=
PM2=![]() ×82=32.
×82=32.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】今年“五一节”前,某商场用60万元购进某种商品,该商品有甲、乙两种包装共500件,其中每件甲包装中有75个A种产品,每个A产品的成本为12元;每件乙包装中有100个B产品,每个B种产品的成本为14元.商场将A产品标价定为每个18元,B产品标价定为每个20元.
(1)甲、乙两种包装的产品各有多少件?
(2)“五一节”商场促销,将A产品按原定标价打9折销售,B种产品按原定标价打8.5折销售,“五一节”期间该产品全部卖完,该商场销售该商品共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,点E在CD上,点F、G在AB上,且AF=FG=BG=DE=CE。以A、B、C、D、E、F、G这7个点中的三个为顶点的三角形中,面积最小的三角形有_________个,面积最大的三角形有__________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
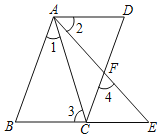
【题目】如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
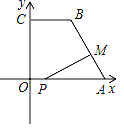
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学公益组织计划购买![]() 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元.
套装共需820元.
(1)求购买一套![]() 套装文具、一套
套装文具、一套![]() 套装各需要多少元?
套装各需要多少元?
(2)根据该公益组织的募捐情况和捐助对象情况,需购买![]() 两种套装共60套,要求购买
两种套装共60套,要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多多少套?
套装最多多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com