
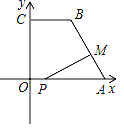
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
【答案】(1)10;(2)中点处;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,利用勾股定理求出
,利用勾股定理求出![]() 的长度;
的长度;
(2)先判断出点![]() 在
在![]() 上,然后表示出
上,然后表示出![]() 即可用三角形的面积公式即可;
即可用三角形的面积公式即可;
(3)![]() 为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
试题解析:
(1)如图1,过点B作BD⊥x轴于点D,
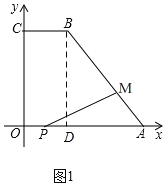
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
(2)∵AB=10,
∴10÷2=5,
![]()
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
![]()
![]()
![]()
![]()
![]()
∴t=5时,S取最大值,此时PA=10t=5,
即:点P在OA的中点处.
(3)由题意可知:![]()
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10t,
若![]() 时,点M在AB上,如图2,
时,点M在AB上,如图2,
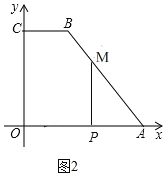
此时AM=2t,
![]()
![]()
![]()
若![]() 时,点M在BC上,如图3,
时,点M在BC上,如图3,
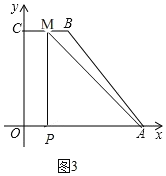
∴CM=142t,OP=t,
∴OP=CM,
∴t=142t,
![]() 当点A是直角顶点时,
当点A是直角顶点时,
此时,∠MAP不可能为![]() 此情况不符合题意;
此情况不符合题意;
当点M是直角顶点时,
若![]() 时,M在AB上,如图4,
时,M在AB上,如图4,
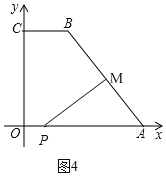
此时,AM=2t,AP=10t
![]()
![]()
![]()
![]()
若![]() 时,点M在BC上,如图5,
时,点M在BC上,如图5,
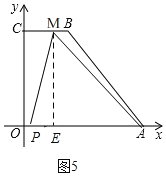
过点M作ME⊥x轴于点E,
此时,CM=142t,OP=t,
∴ME=8,PE=CMOP=143t,
∴EA=10(142t)=2t4,
![]()
![]()
∴∠PME=∠MAP,
∴△PME∽△MAE,
![]()
![]()
∴64=(143t)(2t4),
![]()
![]() 故此情况不存在;
故此情况不存在;
综上所述,t=![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
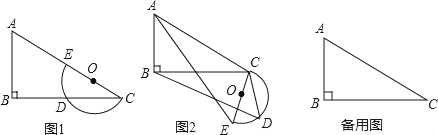
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
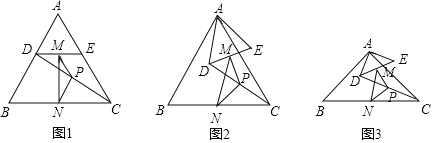
【题目】如图,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
在如图中,线段PM与PN的数量关系是______,∠MPN的度数是______;
(2)探究证明
把△ADE绕点A逆时针方向旋转到如图的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸
若△ABC为直角三角形,∠BAC=90°,AB=AC=12,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图.
①△PMN的是______三角形.
②直接利用①中的结论,求△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
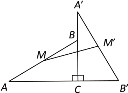
【题目】如图,在Rt△ABC中,∠C=90°,将△ABC绕点C顺时针旋转90°得到△A′B′C,M、M′分别是AB、A′B′的中点,若AC=8,BC=6,则线段MM′的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ∥AB,
∥AB,![]() 与 AB 之间的距离为 2 ,C、D 是直线
与 AB 之间的距离为 2 ,C、D 是直线![]() 上
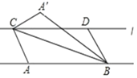
上![]() 两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
两个动点(点 C在 D 点的左侧),且 AB=CD=5.连接 AC、BC、BD,将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形,则此矩形相邻两边之和为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
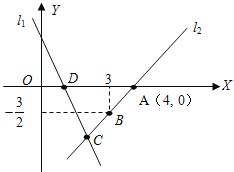
【题目】如图,直线![]() 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
(1)求点D的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线![]() 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
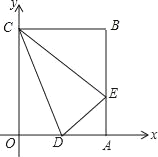
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com