
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
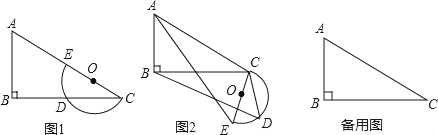
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
【答案】(1)90°,![]() ;(2)无变化;(3)
;(2)无变化;(3)![]() ;(4)BD=
;(4)BD=![]() 或
或![]() .
.
【解析】试题分析:(1)①根据直径的性质,由DE∥AB得![]() 即可解决问题.②求出BD、AE即可解决问题.
即可解决问题.②求出BD、AE即可解决问题.
(2)只要证明△ACE∽△BCD即可.
(3)求出AB、AE,利用△ACE∽△BCD即可解决问题.
(4)分类讨论:①如图5中,当α=90°时,半圆与AC相切,②如图6中,当α=90°+∠ACB时,半圆与BC相切,分别求出BD即可.
试题解析:(1)解:①如图1中,当α=0时,连接DE,则∠CDE=90°.∵∠CDE=∠B=90°,∴DE∥AB,∴![]() =
=![]() .∵BC=n,∴CD=
.∵BC=n,∴CD=![]() .故答案为:90°,
.故答案为:90°,![]() n.
n.
②如图2中,当α=180°时,BD=BC+CD=![]() n,AE=AC+CE=
n,AE=AC+CE=![]() m,∴
m,∴![]() =
=![]() .故答案为:
.故答案为:![]() .
.
(2)如图3中,∵∠ACB=∠DCE,∴∠ACE=∠BCD.∵![]() ,∴△ACE∽△BCD,∴
,∴△ACE∽△BCD,∴![]() .
.
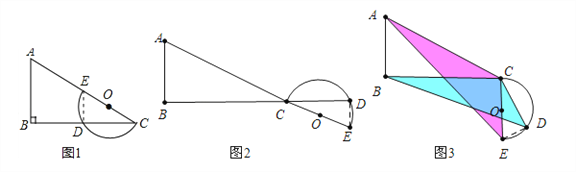
(3)如图4中,当α=∠ACB时.在Rt△ABC中,∵AC=10,BC=8,∴AB=![]() =6.在Rt△ABE中,∵AB=6,BE=BC﹣CE=3,∴AE=
=6.在Rt△ABE中,∵AB=6,BE=BC﹣CE=3,∴AE=![]() =
=![]() =3
=3![]() ,由(2)可知△ACE∽△BCD,∴
,由(2)可知△ACE∽△BCD,∴![]() ,∴
,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .故答案为:
.故答案为:![]() .
.
(4)∵m=6,n=![]() ,∴CE=3,CD=2
,∴CE=3,CD=2![]() ,AB=
,AB=![]() =2,①如图5中,当α=90°时,半圆与AC相切.在Rt△DBC中,BD=
=2,①如图5中,当α=90°时,半圆与AC相切.在Rt△DBC中,BD=![]() =
=![]() =2
=2![]() .
.
②如图6中,当α=90°+∠ACB时,半圆与BC相切,作EM⊥AB于M.∵∠M=∠CBM=∠BCE=90°,∴四边形BCEM是矩形,∴![]() ,∴AM=5,AE=
,∴AM=5,AE=![]() =
=![]() ,由(2)可知
,由(2)可知![]() =
=![]() ,∴BD=
,∴BD=![]() .
.
故答案为:2![]() 或
或![]() .
.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知![]() 中,
中,![]() ,一条直角边为3,如果
,一条直角边为3,如果![]() 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一节”前,某商场用60万元购进某种商品,该商品有甲、乙两种包装共500件,其中每件甲包装中有75个A种产品,每个A产品的成本为12元;每件乙包装中有100个B产品,每个B种产品的成本为14元.商场将A产品标价定为每个18元,B产品标价定为每个20元.
(1)甲、乙两种包装的产品各有多少件?
(2)“五一节”商场促销,将A产品按原定标价打9折销售,B种产品按原定标价打8.5折销售,“五一节”期间该产品全部卖完,该商场销售该商品共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
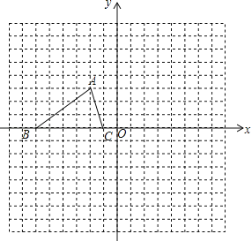
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′的坐标_____;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A″的坐标_____;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,点E在CD上,点F、G在AB上,且AF=FG=BG=DE=CE。以A、B、C、D、E、F、G这7个点中的三个为顶点的三角形中,面积最小的三角形有_________个,面积最大的三角形有__________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
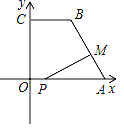
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com