
【题目】如图,![]() 为
为![]() 中的一条射线,点
中的一条射线,点![]() 在边
在边![]() 上,
上,![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
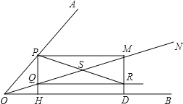
![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 若
若![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据垂直于同一直线的两直线平行可得PH∥MD,再根据平行于同一直线的两直线平行可得PM∥QR,然后求出四边形PQRM是平行四边形,再求出∠MPQ=90°,根据有一个角是直角的平行四边形是矩形证明即可;
(2)根据矩形的对角线互相平分可得PS=![]() PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() .理由如下:
.理由如下:
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,交
,交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
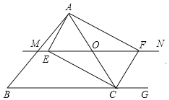
![]() 判断
判断![]() 与
与![]() 的大小关系?并说明理由;
的大小关系?并说明理由;
![]() 当点
当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并说出你的理由;
是矩形?并说出你的理由;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形.直接写出答案,不需说明理由.
是正方形.直接写出答案,不需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在矩形
分别在矩形![]() 边
边![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为正方形时,求
为正方形时,求![]() 的面积;
的面积;
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为菱形时,设
为菱形时,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com