
【题目】如图,菱形ABCD的对角线相交于点0,AC=2,BD=![]() .将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )
.将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据菱形的性质得到∠ABO=∠CBO,AC⊥BD,可证得∠ABC=60°,由折叠的性质得到EF⊥BO,推出△BEF是等边三角形,推出EF是△ABC的中位线,求得EF= ![]() AC=1,求出△BEF和菱形ABCD的面积,即可得出答案.
AC=1,求出△BEF和菱形ABCD的面积,即可得出答案.
解:∵四边形ABCD是菱形,AC=2,![]() ,
,
∴∠ABO=∠CBO,AC⊥BD,AO=1,BO= ![]() ,
,
∴AB=2,
∴∠CBO=∠ABO=30°,
∴∠ABC=60°,
由折叠的性质得,EF⊥BO,
∴∠BEF=∠BFE=60°,EF∥AC,
∴BE=BF,
∴△BEF是等边三角形, EF是△ABC的中位线,
∴EF= ![]() AC=1,
AC=1,
∴△BEF的面积= ![]() EF×
EF×![]() BO=
BO= ![]() ×1×
×1×![]() ×
×![]() =
= ![]()
∵菱形ABCD的面积= ![]() AC×BD=
AC×BD= ![]() ×2×2
×2×2![]()
∴五边形AEFCD的面积=菱形ABCD的面积-△BEF的面积= ![]()
故选:D.


科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分)如下:
甲 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
乙 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
(1)整理、描述数据:按如分数段整理、描述这两组样本数据(请补全表格):
|
|
|
|
|
| |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 | __________ | 0 | 0 | __________ | __________ | __________ |
(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | __________ | 75 |
乙 | 78 | 80.5 | __________ |
得出结论:
(2)估计乙部门生产技能优秀的员工人数为__________;
(3)你认为__________部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,且
上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() .
.
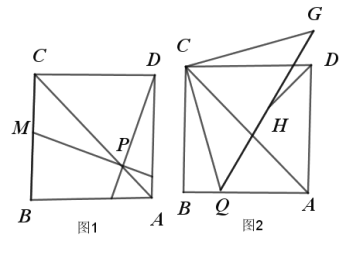
(1)求证:![]() ;
;
(2)已知如图(2),![]() 为
为![]() 上一点,连接
上一点,连接![]() ,并将
,并将![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,试求出
,试求出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( ) 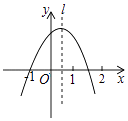
A.①③
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com