【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBEF是菱形？为什么？
【答案】（1）证明见解析；（2）当AB=BC时，四边形DBEF是菱形，理由见解析.
【解析】
试题（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC，然后根据两组对边分别平行的四边形是平行四边形证明.
（2）根据邻边相等的平行四边形是菱形证明．
试题解析：
（1）∵D、E分别是AB、AC的中点，
∴DE是△ABC的中位线.
∴DE∥BC.
又∵EF∥AB，
∴四边形DBFE是平行四边形.
（2）当AB=BC时，四边形DBEF是菱形．
理由如下：
∵D是AB的中点，
∴BD= 
AB.
∵DE是△ABC的中位线，
∴DE= BC.
∵AB=BC，
∴BD=DE.
又∵四边形DBFE是平行四边形，
∴四边形DBFE是菱形．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB= 
BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE= 
BC，成立的个数有（ ）
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，△ABC满足∠BCA＝90°，AC＝BC＝
，点A、C分别在x轴和y轴上，当点A从原点开始沿x轴的正方向运动时，则点C始终在y轴上运动，点B始终在第一象限运动．
（1）当AB∥y轴时，求B点坐标．
（2）随着A、C的运动，当点B落在直线y＝3x上时，求此时A点的坐标．
（3）在（2）的条件下，在y轴上是否存在点D，使以O、A、B、D为顶点的四边形面积是4？如果存在，请直接写出点D的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，∠DOC=2∠ACD=90°．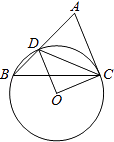
（1）求证：直线AC是圆O的切线；
（2）如果∠ACB=75°，圆O的半径为2，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD，其中AD//BC，AB⊥BC，将DC沿DE折叠，C落于
，
交CB于G，且ABGD为长方形（如图1）；再将纸片展开，将AD沿DF折叠，使A点落在DC上一点
（如图2），在两次折叠过程中，两条折痕DE、DF所成的角为____________度.
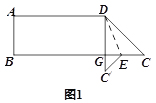
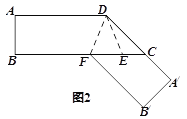
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤．
妈妈：“今天买这两样菜共花了45元，上月买同重量的这两样菜只要36元”；
爸爸：“报纸上说了萝卜的单价上涨50%，排骨单价上涨20%”；
小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少？”
请你通过列方程（组）求解这天萝卜、排骨的单价（单位：元/斤）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】[阅读]
在平面直角坐标系中，以任意两点P（ x1，y1）、Q（x2，y2）为端点的线段中点坐标为（
，
）．
[运用]
（1）如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为 ．
（2）在直角坐标系中，有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．
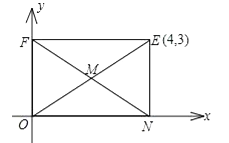
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①所示是一个长为
，宽为
的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．
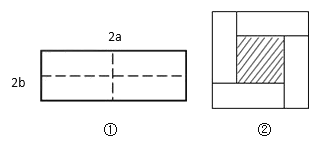
（1）图②中的阴影部分的正方形的边长等于 ．（用含
，
的代数式表示）
（2）请用两种不同的方法列代数式表示图②中阴影部分的面积：
方法①： ．
方法②： ．
（3）观察图②，直接写出
、
、
这三个代数式之间的等量关系．
（4）根据（3）题中的等量关系，若
，
，求图②中阴影部分的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
