
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB= ![]() BC,
BC,
∴AE= ![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵AB= ![]() BC,OB=
BC,OB= ![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE= ![]() AB,
AB,
∴OE= ![]() BC,故④正确.
BC,故④正确.
故答案为:C.
首先根据平行四边形的性质可得到∠ABC=∠ADC=60°,∠BAD=120°,然后结合条件AE平分∠BAD,可得到∠BAE=∠EAD=60°,故此可证明△ABE是等边三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;因为AC⊥AB,所以依据平行四边形的面积公式可得到SABCD=ABAC,故②正确,然后由AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;因为AC⊥AB,所以依据平行四边形的面积公式可得到SABCD=ABAC,故②正确,然后由AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,可证明AB≠OB,故③错误;接下来,依据三角形的中位线的性质定理证明OE=
BD,且BD>BC,可证明AB≠OB,故③错误;接下来,依据三角形的中位线的性质定理证明OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正确.
BC,故④正确.


科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
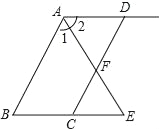
证明:∵AD∥BC(已知)
∴∠2=∠E(___________________________)
∵AE平分∠BAD(已知)
∴∠1=∠2 (_________________________)
∴∠1=∠E(___________________________)
∵∠CFE=∠E(已知)
∴∠1=∠______(______________________)
∴AB∥CD(_________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.
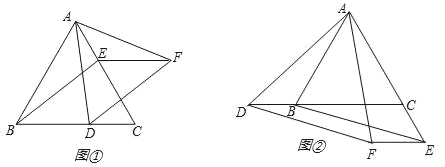
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.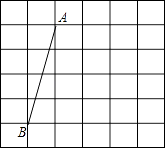
(1)将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;
(2)求证:△AOB≌△B′OA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,衢江河畔,鸟语花香,柳条摇曳.为给衢州市民提供更好的休闲锻炼环境,决定对衢江沿河步行道修建改造.据了解我市步行道改造工程路线约12千米,若该任务由甲、乙两工程队先后接力完成,甲工程队每天修建0.04千米,乙工程队每天修建0.02千米,则两工程队共需修建500天,求甲、乙两工程队分别修建步行道多少千米.
根据题意,小刚同学列出了一个不完整的方程组![]() .
.
(1)根据小刚同学所列的方程组,请你分别指出未知数![]() ,
,![]() 表示的意义.
表示的意义.![]() 表示 ;
表示 ;![]() 表示 ;
表示 ;
(2)小红同学的做法是:“设甲工程队修建步行道![]() 千米,乙工程队修建步行道
千米,乙工程队修建步行道![]() 千米”,请你利用小红同学设的未知数解决问题.
千米”,请你利用小红同学设的未知数解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,点M、N分别为四边形ABCD边AD、BC的中点,则四边形BNDM的面积与四边形ABCD的面积关系是 . 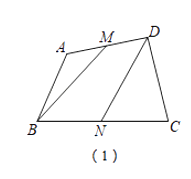
(2)如图②,在四边形ABCD中,点M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于点Q,若S△四边形MPNQ=10,则S△ABP+S△DCQ的值为多少?
(3)问题解决
在矩形ABCD中,AD=2,DC=4,点M、N为AB上两点,且满足BN=2AM=2MN,连接MC、MD.若点P为CD上任意一点,连接AP、NP,使得AP与DM交于点E,NP与MC交于点F,则四边形MEPF的面积是否存最大值?若存在,请求出最大面积;若不存在,请说明理由.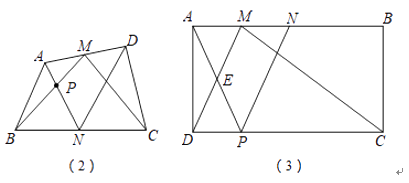
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com