
【题目】问题探究:
(1)如图①,点M、N分别为四边形ABCD边AD、BC的中点,则四边形BNDM的面积与四边形ABCD的面积关系是 . 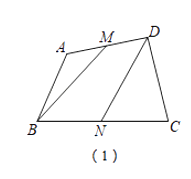
(2)如图②,在四边形ABCD中,点M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于点Q,若S△四边形MPNQ=10,则S△ABP+S△DCQ的值为多少?
(3)问题解决
在矩形ABCD中,AD=2,DC=4,点M、N为AB上两点,且满足BN=2AM=2MN,连接MC、MD.若点P为CD上任意一点,连接AP、NP,使得AP与DM交于点E,NP与MC交于点F,则四边形MEPF的面积是否存最大值?若存在,请求出最大面积;若不存在,请说明理由.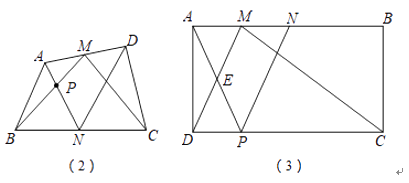
【答案】
(1)S四边形BNDM= ![]() S四边形ABCD
S四边形ABCD
(2)解:连接BD. 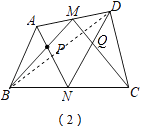
∵M、N是AD、BC中点,
∴S△ABM=S△BDM,S△BDN=S△CDN,(等底同高的两个三角形面积相等)
∴S四边形BMDN= ![]() S四边形ABCD.
S四边形ABCD.
同理,S四边形ANCM= ![]() S四边形ABCD.
S四边形ABCD.
∴S四边形ANCM+S四边形BMDN=S四边形ABCD,
∴S四边形MPNQ=S△ABP+S△CDQ=10;
(3)连接PM, 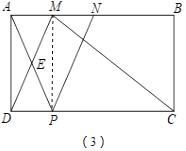
设DP=x,则PC=4﹣x,
∵AM∥DP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() 且S△APM=
且S△APM= ![]() AMAD=1,
AMAD=1,
∴S△MPE= ![]() ,
,
同理可得,S△MPF= ![]() ,
,
∴S= ![]() +
+ ![]() =2﹣
=2﹣ ![]() ﹣
﹣ ![]() =2﹣
=2﹣ ![]() =2+
=2+ ![]() ≤2﹣
≤2﹣ ![]() =
= ![]() ,
,
当x=2时,上式等号成立,
∴S的最大值为: ![]() .
.
【解析】解:(1)S四边形BNDM= ![]() S四边形ABCD,
S四边形ABCD,
理由:连接BD, 
∵点M、N分别为四边形ABCD边AD、BC的中点,
∴S△BDM= ![]() S△ABD,S△BDN=
S△ABD,S△BDN= ![]() S△BCD,
S△BCD,
∴S四边形BNDM=S△BDM+S△BDN= ![]() (S△ABD+S△BCD)=
(S△ABD+S△BCD)= ![]() S四边形ABCD,
S四边形ABCD,
(2)连接BD. 
∵M、N是AD、BC中点,
∴S△ABM=S△BDM,S△BDN=S△CDN,(等底同高的两个三角形面积相等)
∴S四边形BMDN= ![]() S四边形ABCD.
S四边形ABCD.
同理,S四边形ANCM= ![]() S四边形ABCD.
S四边形ABCD.
∴S四边形ANCM+S四边形BMDN=S四边形ABCD,
∴S四边形MPNQ=S△ABP+S△CDQ=10;
(3)连接PM, 
设DP=x,则PC=4﹣x,
∵AM∥DP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() 且S△APM=
且S△APM= ![]() AMAD=1,
AMAD=1,
∴S△MPE= ![]() ,
,
同理可得,S△MPF= ![]() ,
,
∴S= ![]() +
+ ![]() =2﹣
=2﹣ ![]() ﹣
﹣ ![]() =2﹣
=2﹣ ![]() =2+
=2+ ![]() ≤2﹣
≤2﹣ ![]() =
= ![]() ,
,
当x=2时,上式等号成立,
∴S的最大值为: ![]() .
.
所以答案是:(1)S四边形BNDM= ![]() S四边形ABCD;(2)10;(3)存在,最大值为
S四边形ABCD;(2)10;(3)存在,最大值为![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲骑自行车从
两地,甲骑自行车从![]() 地到
地到![]() 地;乙骑自行车从
地;乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题:
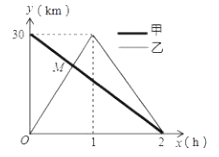
(1)求出甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2)求出点![]() 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过![]() 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导“低碳生活”,常选择以自行车作为代步工具.如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,车轮半径28cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2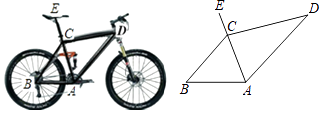
(1)求车座点E到地面的距离;(结果精确到1cm)
(2)求车把点D到车架档直线AB的距离.(结果精确到1cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
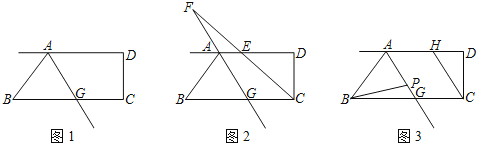
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=![]() ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
(1)当AB∥y轴时,求B点坐标.
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.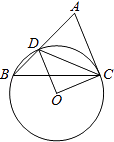
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(![]() ,
,![]() ).
).
[运用]
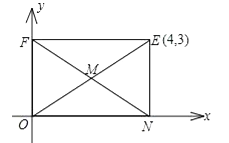
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com