
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲骑自行车从
两地,甲骑自行车从![]() 地到
地到![]() 地;乙骑自行车从
地;乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题:
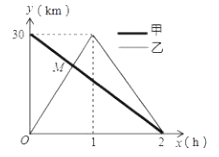
(1)求出甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2)求出点![]() 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过![]() 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2) 点M的坐标是(
;(2) 点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;(3)
h第一次相遇,此时离点B的距离是20km;(3) ![]() 当或
当或![]() ≤x≤2.
≤x≤2.
【解析】
(1) 根据函数图象就可以得出A, C点坐标,用待定系数法可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2) 根据函数图象求出OC的解析式,求出OC与AB的交点可得M点坐标, 根据图像可得M的坐标表示的含义;
(3) 分情况讨论,当![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3,分别求出x的值可以得出结论.
≤3,分别求出x的值可以得出结论.
解:如图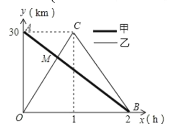
可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式即为AC的函数表达式,
之间的函数表达式即为AC的函数表达式,
其经过点A(0,30),B(2,0),
设其表达式为:![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() .
.
(2) 设OC的解析式为![]() ,其经过点C(1,30),
,其经过点C(1,30),
可得![]() =30,
=30,![]()
![]() ;
;
设BC的解析式为![]() ,其经过点C(1,30),B(2,0),
,其经过点C(1,30),B(2,0),
可得:![]() ,解得
,解得![]() ,
,
![]()
![]()
![]()
![]()
可得M点为AB与OC的交点,![]() =
=![]() 可得-15x+30=30x,
可得-15x+30=30x,
解得:x=![]() ,
,![]()
![]() =
=![]() =20,
=20,
![]() 点M的坐标是(
点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;
h第一次相遇,此时离点B的距离是20km;
(3)分情况讨论:
①![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3时
≤3时
![]() 解得:
解得:![]()
②(-30x+60)-(15x+30)≤3
解得:x≥![]()
![]()
![]() ≤x≤2
≤x≤2
综上所述:![]() 当或
当或![]() ≤x≤2两人能够用无线对讲机保持联系.
≤x≤2两人能够用无线对讲机保持联系.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
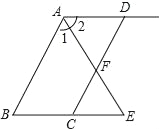
证明:∵AD∥BC(已知)
∴∠2=∠E(___________________________)
∵AE平分∠BAD(已知)
∴∠1=∠2 (_________________________)
∴∠1=∠E(___________________________)
∵∠CFE=∠E(已知)
∴∠1=∠______(______________________)
∴AB∥CD(_________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 直线
直线![]() ,垂足为
,垂足为![]() ,
,![]() 如图放置,过点
如图放置,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,在
,在![]() 内取一点
内取一点![]() ,连接
,连接![]() ,
,![]() .
.
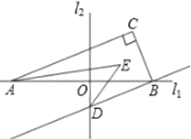
(1)若![]() ,
,![]() ,则
,则![]() _______.
_______.
(2)若![]() ,
,![]() ,则
,则![]() _______°.(用含
_______°.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,![]() 时注满水槽,水槽内水面的高度
时注满水槽,水槽内水面的高度![]() 与注水时间
与注水时间![]() 之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.
之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
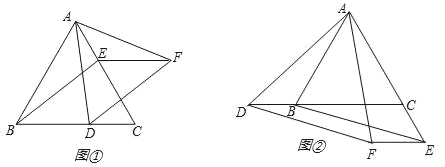
【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.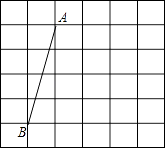
(1)将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;
(2)求证:△AOB≌△B′OA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,点M、N分别为四边形ABCD边AD、BC的中点,则四边形BNDM的面积与四边形ABCD的面积关系是 . 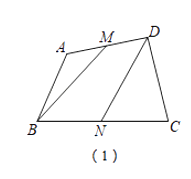
(2)如图②,在四边形ABCD中,点M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于点Q,若S△四边形MPNQ=10,则S△ABP+S△DCQ的值为多少?
(3)问题解决
在矩形ABCD中,AD=2,DC=4,点M、N为AB上两点,且满足BN=2AM=2MN,连接MC、MD.若点P为CD上任意一点,连接AP、NP,使得AP与DM交于点E,NP与MC交于点F,则四边形MEPF的面积是否存最大值?若存在,请求出最大面积;若不存在,请说明理由.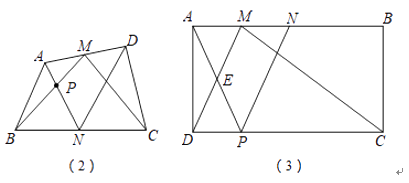
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com