
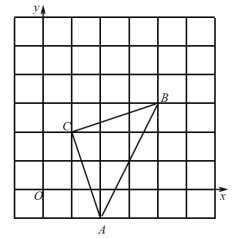
����Ŀ����ͼ����ֱ������ϵ�У���ABC�����BCA��90�㣬AC��BC��![]() ����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
��1����AB��y��ʱ����B�����꣮
��2������A��C���˶�������B����ֱ��y��3x��ʱ�����ʱA������꣮
��3���ڣ�2���������£���y�����Ƿ���ڵ�D��ʹ��O��A��B��DΪ������ı��������4��������ڣ���ֱ��д����D�����ꣻ��������ڣ���˵�����ɣ�

���𰸡���1����B����Ϊ��![]() ��
��![]() ����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
��������
��1�����ݹ��ɶ������ɵ�AB�ij������ݹ��ɶ������ɵ�AO�ij����ɵ�B�����ꣻ
��2������ȫ�������ε��ж������ʣ��ɵ�BE��OC��x��EC��OA��x�����ݹ��ɶ������ɵ�x�ij����ɵ�A�����ꣻ
��3���������ۣ���D��y����������ϣ���D��y��ĸ������ϣ���������ĺͲ�ɵù���y�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��1���ߡ�BCA��90�㣬AC��BC��![]() ��
��
���BAC��45�㣬AB��![]() ��
��![]()
��AB��y�ᣬ
���BAO��90�㣽��COA
���CAO��45�㣽��OCA
��CO��AO
��AO2+CO2��AC2��
��2AO2��5
��AO��![]()
���B������![]() ��
��![]() ��
��
��2����ͼ������B����BE��y�ᣬ����Ϊ��E��
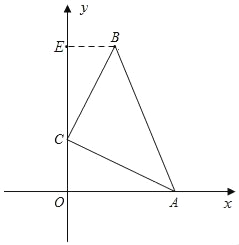
�ߡ�BCE+��ACO��90�㣬��ACO+��CAO��90��
���BCE����CAO����AC��BC����BEO����AOC
���AOC�ա�CEB��AAS��
��BE��CO��AO��CE
�ߵ�B����ֱ��y��3x��
����B��x��3x��
��BE��x��OC��OE��3x��
��CE��OA��2x��
��OA2+OC2��AC2
�ࣨ2x��2+x2��5
��x��1
��OA��2x��2
���A��2��0��
��3�����D��0��y��
����D��y���������ϣ���ͼ������OB��
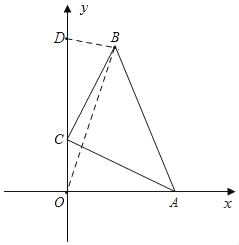
��S�ı���ABDO��S��AOB+S��BDO��4
��![]() ��y��1+
��y��1+![]() ��2��3��4
��2��3��4
��y��2
���D��0��2��
����D��y�Ḻ�����ϣ���ͼ������OB��
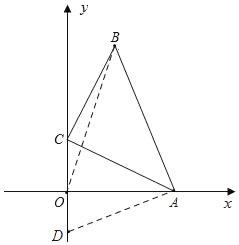
��S�ı���ABDO��S��AOB+S��ADO��4
��![]() ��2��3+
��2��3+![]() ��2������y����4
��2������y����4
��y����1
���D������0����1��.
����ڵ�D����D����Ϊ��0��2����0����1��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
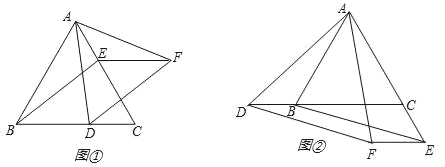
����Ŀ����ͼ�٣���ABC�ǵȱ������Σ�D��E�ֱ�Ϊ��BC��AC�ϵĵ㣬��BD��CE����D��BE��ƽ���ߣ���E��BC��ƽ���ߣ����ǽ��ڵ�F������AF��
��1����֤����ABE�ա�CAD��
��2�����жϡ�ADF����״����˵�����ɣ�
��3������D��E�ֱ���Ϊ��CB���ӳ��ߺ�AC���ӳ����ϵĵ㣬�����������䣨��ͼ�ڣ������ADF����״�Ƿ�ı䣬˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
��ش���������:
ʱ�� | ��һ��7��00��8��00 | �ڶ���7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 |
��Ҫ�������г�ȴδ������������ˣ� | 1500 | 1200 | 1300 | 1300 | 1200 |
��1�������е�������ݣ�����������λ�������٣�
��2�����������������ƽ��ÿ����7:00-8:00 :��Ҫ���ù������г���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽����
��1����ͼ�٣���M��N�ֱ�Ϊ�ı���ABCD��AD��BC���е㣬���ı���BNDM��������ı���ABCD�������ϵ�� �� 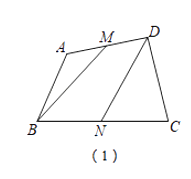
��2����ͼ�ڣ����ı���ABCD�У���M��N�ֱ�ΪAD��BC���е㣬MB��AN�ڵ�P��MC��DN�ڵ�Q����S���ı���MPNQ=10����S��ABP+S��DCQ��ֵΪ���٣�
��3��������
�ھ���ABCD�У�AD=2��DC=4����M��NΪAB�����㣬������BN=2AM=2MN������MC��MD������PΪCD������һ�㣬����AP��NP��ʹ��AP��DM���ڵ�E��NP��MC���ڵ�F�����ı���MEPF������Ƿ�����ֵ�������ڣ���������������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľ��̵����۹�����ͬ��A��B����Ʒ�Ƶļ�����������2��AƷ�ƺ�3��BƷ�Ƶļ���������156Ԫ������3��AƷ�ƺ�1��BƷ�Ƶļ���������122Ԫ��
��1����������Ʒ�Ƽ������ĵ�����
��2��ѧУ��ѧǰϦ�����̵�������ּ�������չ�˴����������취������AƷ�Ƽ�������ԭ�۵İ���������BƷ�Ƽ���������5���IJ��ְ�ԭ�۵������������蹺��x��AƷ�Ƶļ�������Ҫy1Ԫ������x��x��5����BƷ�Ƶļ�������Ҫy2Ԫ���ֱ����y1��y2����x�ĺ�����ϵʽ��
��3������Ҫ����50��������ʱ��������Ʒ�Ƶļ����������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E��F�ֱ���AB��BC��CA���е㣬AH�DZ�BC�ϵĸߣ�
��1����֤���ı���ADEF��ƽ���ı��Σ�
��2����֤����DHF=��DEF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����վ�۲�һ��ɳ�����ӷ�����������ȫ��������ʼʱ���ٰ�һ�����ٶ�����������������Į��ʱ����������ıȽϿ���һ��ʱ��������ٱ��ֲ�������ɳ��������������ʱ������ٿ�ʼ��С������ֹͣ����ͼ��ʾ�Ƿ�����ʱ��֮��Ĺ�ϵ��ͼ�������ͼ��ش��������⣺

(1)ɳ�����ӿ�ʼ�����������������˶ʱ�䣿
(2)��ͼ���Ͽ�����������һ��ʱ�������ıȽϿ������ӵ��ٶ��Ƕ��٣�
(3)��������һʱ��α��ֲ����������˶ʱ�䣿
(4)���ٴӿ�ʼ��С������ֹͣ������ÿСʱ��С���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬����E��EF��AB����BC�ڵ�F��
��1����֤���ı���DBFE��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ���ı���DBEF�����Σ�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У�![]() �Ķ��㶼��������ϣ����У�
�Ķ��㶼��������ϣ����У�![]() ������Ϊ
������Ϊ![]() ��
��
��1�����![]() ��
��![]() �����꣺
�����꣺![]() ��____��____����
��____��____����![]() ��____��____��
��____��____��
��2����![]() ������ƽ��
������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ��õ�
����λ���ȣ��õ�![]() ������
������![]() ��
��
��3���������������![]() ��___��___����
��___��___����![]() ��___��___����
��___��___����![]() ��___��___����
��___��___����
��4����![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com