
【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
【答案】②④⑤
【解析】解:由图象可知,抛物线开口向上,则a>0, 顶点在y轴右侧,则b<0,
抛物线与y轴交于负半轴,则c<0,
∴abc>0,故①错误;
∵抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,
∴抛物线y=ax2+bx+c过点(3,0),
∴当x=3时,y=9a+3b+c=0,
∵a>0,
∴10a+3b+c>0,故②正确;
∵对称轴为x=1,且开口向上,
∴离对称轴水平距离越大,函数值越大,
∴y1<y2 , 故③错误;
当x=﹣ ![]() 时,y=a(﹣
时,y=a(﹣ ![]() )2+b(﹣
)2+b(﹣ ![]() )+c=
)+c= ![]() =
= ![]() ,
,
∵当x=﹣1时,y=a﹣b+c=0,
∴当x=﹣ ![]() 时,y=a(﹣
时,y=a(﹣ ![]() )2+b(﹣
)2+b(﹣ ![]() )+c=0,
)+c=0,
即无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0),故④正确;
,0),故④正确;
x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,
又∵x=1时函数取得最小值,
∴am2+bm+c≥a+b+c,即am2+bm≥a+b,
∵b=﹣2a,
∴am2+bm+a≥0,故⑤正确;
所以答案是:②④⑤.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点分别在四条平行线 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 上,这四条直线中相邻两条之间的距离依次为
上,这四条直线中相邻两条之间的距离依次为 ![]() 、
、 ![]() 、
、 ![]() (
( ![]() >0,
>0, ![]() >0,
>0, ![]() >0).
>0).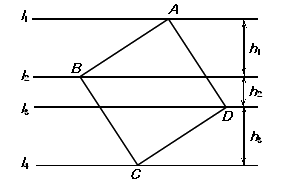
(1)求证: ![]() =
= ![]() ;
;
(2)设正方形ABCD的面积为S,求证:S= ![]() ;
;
(3)若 ![]() ,当
,当 ![]() 变化时,说明正方形ABCD的面积S随
变化时,说明正方形ABCD的面积S随 ![]() 的变化情况.
的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点0,AC=2,BD=![]() .将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )
.将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(﹣ ![]() ,y1),(﹣
,y1),(﹣ ![]() ,y2),(﹣
,y2),(﹣ ![]() ,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( )
,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( ) 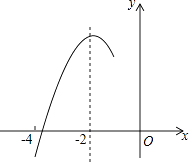
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
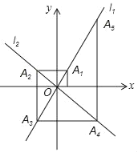
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b交x轴于点A,交y轴于点B,且a,b满足a=![]() +4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.
+4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.
(1)a= ,b= ,C坐标为 ;
(2)如图1,k=﹣1时,求点D的坐标;
(3)如图2,在(2)的条件下,点M是直线y=kx﹣4k上一点,连接AM,将AM绕A顺时针旋转90°得AQ,OQ最小值为 .
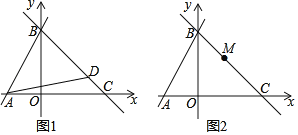
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河大附中初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(m,0),B(n,0),C(﹣1,2),且满足式|m+2|+(m+n﹣2)2=0.
(1)求出m,n的值.
(2)①在x轴的正半轴上存在一点M,使△COM的面积等于△ABC的面积的一半,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积等于△ABC的面积的一半仍然成立,若存在,请直接在所给的横线上写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,![]() 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com