【题目】河大附中初一年级有350名同学去春游，已知2辆A型车和1辆B型车可以载学生100人；1辆A型车和2辆B型车可以载学生110人．
（1）A、B型车每辆可分别载学生多少人？
（2）若租一辆A需要100元，一辆B需120元，请你设计租车方案，使得恰好运送完学生并且租车费用最少．
【答案】（1）A、B型车每辆可分别载学生30人，40人；（2）租用1辆A型8辆B型车花费最少为1060元．
【解析】
（1）根据载客量，可得方程组，根据解方程组，可得答案；
（2）根据题意列出方程，可得答案．
（1）设A、B型车每辆可分别载学生x，y人，
可得：
，
解得：
，
答：A、B型车每辆可分别载学生30人，40人；
（2）设租用A型a辆，B型b辆，
可得：30a+40b＝350，
因为a，b为正整数，所以方程的解为：
，
，
，
方案一：A型1辆，B型8辆，费用：100×1+120×8＝1060元；
方案二：A型5辆，B型5辆，费用：100×5+120×5＝1100元；
方案三：A型9辆，B型2辆，费用：100×9+120×2＝1140元；
所以租用1辆A型8辆B型车花费最少为1060元．
科目：初中数学 来源： 题型：
【题目】正方形
中，
为对角线
上一点，且
，
交
于
，延长
交
于
．
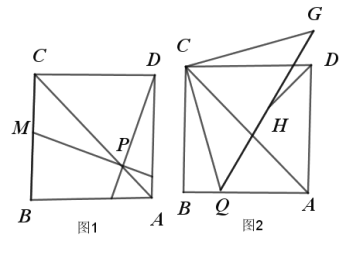
（1）求证：
；
（2）已知如图（2），
为上一点，连接
，并将逆时针旋转
至
，连接
，
为
的中点，连接
，试求出
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（ ）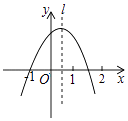 
A.①③
B.②③
C.②④
D.②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c过点（﹣1，0），且对称轴为直线x=1，有下列结论： ①abc＜0；②10a+3b+c＞0；③抛物线经过点（4，y1）与点（﹣3，y2），则y1＞y2；④无论a，b，c取何值，抛物线都经过同一个点（﹣ 
，0）；⑤am2+bm+a≥0，其中所有正确的结论是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探索题：图a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．
（1）请用两种不同的方法，求图b中阴影部分的面积：
方法1： ； 方法2： ；
（2）观察图b，写出代数式
， 
， 
之间的等量关系，并通过计算验证；
（3）根据（2）题中的等量关系，解决如下问题：若
， 
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 
、 
是关于 
的方程 
的两个不相等的实数根.
（1）求实数 
的取值范围;
（2）已知等腰 
的一边长为7，若 、 恰好是 另外两边长，求这个三角形的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图．AD∥BE，∠1＝∠2，求证：∠A＝∠E．请完成解答过程．
证明：∵AD∥BE（已知）
∴∠A＝∠ （ ）
又∵∠1＝∠2（已知）
∴AC∥ （ ）
∴∠3＝∠ （两直线平行，内错角相等）
∴∠A＝∠E（等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数 
的图象与 
轴交于A、B两点(A在B的左侧)，与 
轴交于点C，顶点为D．
（1）求点A、B的坐标，并在下面直角坐标系中画出该二次函数的大致图象；
（2）设一次函数 
的图象经过B、D两点，请直接写出满足 
的 的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
