练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知 、 是关于 的方程 的两个不相等的实数根.
    （1）求实数 的取值范围;
    （2）已知等腰 的一边长为7，若 、 恰好是 另外两边长，求这个三角形的周长.

    【答案】
    （1）解：由题意得△=4（m+1）2﹣4（m2+5）=8m－16＞0，解得：m＞2；
    （2）解：由题意，∵x1≠x2时，∴只能取x1=7或x2=7，即7是方程的一个根，将x=7代入得：49﹣14（m+1）+m2+5=0，解得：m=4或m=10．
    当m=4时，方程的另一个根为3，此时三角形三边分别为7、7、3，周长为17；
    当m=10时，方程的另一个根为15，此时不能构成三角形；
    故三角形的周长为17．
    【解析】（1）二次项系数不含字母，由判别式△>0，可求出m范围；（2）需分类讨论，由等腰三角形的性质可得出7是方程的一个根，代入方程，求出m的值，再验证是否构成三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．

    解：设x2－4x=y

    原式=（y+2）（y+6）+4 （第一步）

    =y2+8y+16 （第二步）

    =（y+4）2（第三步）

    =（x2－4x+4）2（第四步）

    回答下列问题：

    （1）该同学第二步到第三步运用了因式分解的_______．

    A．提取公因式

    B．平方差公式

    C．两数和的完全平方公式

    D．两数差的完全平方公式

    （2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．

    （3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣2，与x轴的一个交点在（﹣3，0）和（﹣4，0）之间，其部分图象如图所示，则下列结论：①4a﹣b=0；②c＜0；③﹣3a+c＞0；④4a﹣2b＞at2+bt（t为实数）；⑤点（﹣ ，y1），（﹣ ，y2），（﹣ ，y3）是该抛物线上的点，则y1＜y2＜y3 ， 正确的个数有（ ）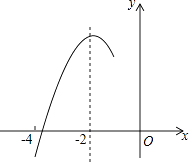
    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

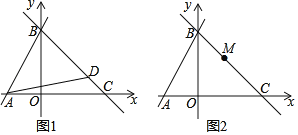
    【题目】如图，直线y＝ax+b交x轴于点A，交y轴于点B，且a，b满足a＝+4，直线y＝kx﹣4k过定点C，点D为直线y＝kx﹣4k上一点，∠DAB＝45°．

    （1）a＝　 　，b＝　 　，C坐标为　 　；

    （2）如图1，k＝﹣1时，求点D的坐标；

    （3）如图2，在（2）的条件下，点M是直线y＝kx﹣4k上一点，连接AM，将AM绕A顺时针旋转90°得AQ，OQ最小值为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】河大附中初一年级有350名同学去春游，已知2辆A型车和1辆B型车可以载学生100人；1辆A型车和2辆B型车可以载学生110人．

    （1）A、B型车每辆可分别载学生多少人？

    （2）若租一辆A需要100元，一辆B需120元，请你设计租车方案，使得恰好运送完学生并且租车费用最少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且经A（1，0）、B（0，﹣3）两点．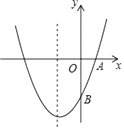

    （1）求抛物线的解析式；
    （2）在抛物线的对称轴x=﹣1上，是否存在点M，使它到点A的距离与到点B的距离之和最小，如果存在求出点M的坐标，如果不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，A（m，0），B（n，0），C（﹣1，2），且满足式|m+2|+（m+n﹣2）2＝0．

    （1）求出m，n的值．

    （2）①在x轴的正半轴上存在一点M，使△COM的面积等于△ABC的面积的一半，求出点M的坐标；

    ②在坐标轴的其它位置是否存在点M，使△COM的面积等于△ABC的面积的一半仍然成立，若存在，请直接在所给的横线上写出符合条件的点M的坐标；

    （3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分∠AOP，OF⊥OE，当点P运动时，的值是否会改变？若不变，求其值；若改变，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC三个顶点的位置如图所示，现将△ABC平移，使点A移动到点A'，点B、C的对应点分别是点B'、C'．

    （1）△ABC的面积是　 　；

    （2）画出平移后的△A'B'C'；

    （3）若连接AA'、CC′，这两条线段的关系是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

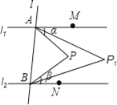
    【题目】如图，直线l1∥l2，直线l与l1、l2分别交于A、B两点，点M、N分别在l1、l2上，点M、N、P均在l的同侧（点P不在l1、l2上），若∠PAM=α，∠PBN=β．

    （1）当点P在l1与l2之间时．

    ①求∠APB的大小（用含α、β的代数式表示）；

    ②若∠PAM的平分线与∠PBN的平分线交于点P1，∠P1AM的平分线与∠P1BN的平分线交于点P2，…，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn，则∠AP1B=　　，∠APnB=　　．（用含α、β的代数式表示，其中n为正整数）

    （2）当点P不在l1与l2之间时．

    若∠PAM的平分线与∠PBN的平分线交于点P，∠P1AM的平分线与∠P1BN的平分线交于点P2，…，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn，请直接写出∠APnB的大小．（用含α、β的代数式表示，其中n为正整数）

    查看答案和解析>>

    同步练习册答案