
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(﹣ ![]() ,y1),(﹣
,y1),(﹣ ![]() ,y2),(﹣
,y2),(﹣ ![]() ,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( )
,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( ) 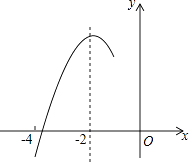
A.4个
B.3个
C.2个
D.1个
【答案】B
【解析】解:∵抛物线的对称轴为直线x=﹣ ![]() =﹣2, ∴4a﹣b=0,所以①正确;
=﹣2, ∴4a﹣b=0,所以①正确;
∵与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,
∴由抛物线的对称性知,另一个交点在(﹣1,0)和(0,0)之间,
∴抛物线与y轴的交点在y轴的负半轴,即c<0,故②正确;
∵由②知,x=﹣1时y>0,且b=4a,
即a﹣b+c=a﹣4a+c=﹣3a+c>0,
所以③正确;
由函数图象知当x=﹣2时,函数取得最大值,
∴4a﹣2b+c≥at2+bt+c,
即4a﹣2b≥at2+bt(t为实数),故④错误;
∵抛物线的开口向下,且对称轴为直线x=﹣2,
∴抛物线上离对称轴水平距离越小,函数值越大,
∴y1<y3<y2 , 故⑤错误;
故选:B.
【考点精析】根据题目的已知条件,利用二次函数的性质和二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可变形为
b2=0可变形为
![]() ,
,
根据a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( ) 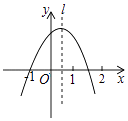
A.①③
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 ![]() 、
、 ![]() 是关于
是关于 ![]() 的方程
的方程 ![]() 的两个不相等的实数根.
的两个不相等的实数根.
(1)求实数 ![]() 的取值范围;
的取值范围;
(2)已知等腰 ![]() 的一边长为7,若
的一边长为7,若 ![]() 、
、 ![]() 恰好是
恰好是 ![]() 另外两边长,求这个三角形的周长.
另外两边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各点,并将各组内的这些点依次用线段连接起来.

①![]() ,
,![]() ,
,![]() ;②
;②![]() ,
,![]() ,
,![]() ,
,![]() .
.
观察所描出的图形,解答下列问题:
(1)坐标轴上的点有_________,![]() 轴上的点_______坐标等于零,
轴上的点_______坐标等于零,![]() 轴上的点_____坐标等于零.
轴上的点_____坐标等于零.
(2)线段![]() 与
与![]() 轴_______,点
轴_______,点![]() 和点
和点![]() _______坐标相同,线段
_______坐标相同,线段![]() 上其他点_____坐标相同.
上其他点_____坐标相同.
(3)线段![]() 与
与![]() 轴_______,点
轴_______,点![]() 和点
和点![]() _______坐标相同,线段
_______坐标相同,线段![]() 上其他点_____坐标相同.
上其他点_____坐标相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com