Question

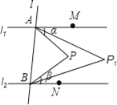
【题目】如图，直线l1∥l2，直线l与l1、l2分别交于A、B两点，点M、N分别在l1、l2上，点M、N、P均在l的同侧（点P不在l1、l2上），若∠PAM=α，∠PBN=β．

（1）当点P在l1与l2之间时．

①求∠APB的大小（用含α、β的代数式表示）；

②若∠PAM的平分线与∠PBN的平分线交于点P1，∠P1AM的平分线与∠P1BN的平分线交于点P2，…，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn，则∠AP1B=　　，∠APnB=　　．（用含α、β的代数式表示，其中n为正整数）

（2）当点P不在l1与l2之间时．

若∠PAM的平分线与∠PBN的平分线交于点P，∠P1AM的平分线与∠P1BN的平分线交于点P2，…，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn，请直接写出∠APnB的大小．（用含α、β的代数式表示，其中n为正整数）

Answer 1

【答案】（1）①∠APB=α+β; ②∠AP1B=（α+β）；∠APnB=;（2）∠ApnB=

【解析】

（1）过点P作PQ∥l1交AB于Q，则∠APQ=∠MAP=α，由∠APQ=∠MAP=α①，∠QPB=∠PBN=β②，①+②即可解决问题．

（2）利用（1）的结论即可解决问题,分两种情形写出结论即可．

（1）①过点P作PQ∥l1交AB于Q，则∠APQ=∠MAP=α … ①

∵l1∥l2，

∴PQ∥l2，

∴∠QPB=∠PBN=β … ②，

①+②得∠APQ+∠BPQ=∠MAP+∠PBN，

∴∠APB=α+β．

由上可知∠P1=（α+β），∠p2=（α+β），∠p3=（α+β）

∴∠APnB=．

故∠AP1B=（α+β）；∠APnB=

（2）当P在l1上方时，β＞α，∠APnB=．

当点P在l2下方时，α＞β，∠ApnB=．

故 ∠ApnB=