
【题目】为提高农民收入,某区一水果公园引进一种新型蟠桃,蟠桃进价为每公斤40元.上市后通过一段时间的试营销发现:当蟠桃销售单价在每公斤40元至90元之间(含40元和90元)时,每月的销售量![]() (公斤)与销售单价
(公斤)与销售单价![]() (元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(1)求![]() 与
与![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2)如果想要每月获得2400元的利润,那么销售单价应定为每公斤多少元?

科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(m,0),B(n,0),C(﹣1,2),且满足式|m+2|+(m+n﹣2)2=0.
(1)求出m,n的值.
(2)①在x轴的正半轴上存在一点M,使△COM的面积等于△ABC的面积的一半,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积等于△ABC的面积的一半仍然成立,若存在,请直接在所给的横线上写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,![]() 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
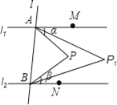
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:AC=ED;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
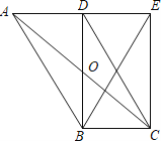
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从![]() 地出发前往
地出发前往![]() 地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达
地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达![]() 地.下图是甲、乙两车离开
地.下图是甲、乙两车离开![]() 地的路程
地的路程![]() 与时间
与时间![]() 之间的函数图象.
之间的函数图象.

(1)甲车每小时行驶_________千米,![]() 的值为________.
的值为________.
(2)求甲车再次行驶过程中![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)甲、乙两车离开![]() 地的路程差为8千米时,直接写出
地的路程差为8千米时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com