
【题目】如图,一次函数 ![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
【答案】
(1)解:∵ ![]() 分别交y轴、x轴于A.、B两点,
分别交y轴、x轴于A.、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=x+bx+c得c=2,
将x=4,y=0,c=2代入y=x+bx+c得0=16+4b+2,解得b= ![]() ,
,
∴抛物线解析式为: ![]()
(2)解:如图1,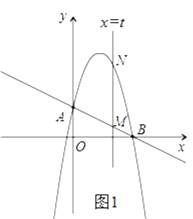
由题意可知,直线MN即是直线 ![]() ,
,
∵点M在直线 ![]() 上,点N在抛物线
上,点N在抛物线 ![]() 上,
上,
∴点M、N的坐标分别为 ![]() 、
、 ![]() ,
,
∵在第一象限中,点N在点M的上方,
∴MN= ![]() ,
,
∴当 ![]() 时,MN最长=4;
时,MN最长=4;
(3)解:由(2)可知,A(0,2),M(2,1),N(2,5).
以A. M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如图2所示:
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a2|=4,解得a1=6,a2=2,
从而D1为(0,6)或D2(0,2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
由D1、D2、M、N的坐标可求得直线D1N的解析式为:y= ![]() x+6,直线D2M的解析式为:y=
x+6,直线D2M的解析式为:y= ![]() x2,
x2,
由  解得
解得 ![]() ,
,
∴D3的坐标为:(4,4),
综上所述,所求的D点坐标为(0,6),(0,2)或(4,4)
【解析】(1)通过直线解析式求出A、B 两点坐标,代入抛物线解析式,运用待定系数法求出抛物线解析式;(2)最值问题可构建以M的横坐标t为自变量的函数,用t的代数式表示竖直线段MN ,应用配方法求出最值;(3)以A. M、N、D为顶点作平行四边形,D点的位置需分类讨论,分别以AM、AN、MN为对角线,另两线段为边,作出平行四边形,共三种情况,利用直线的交点构建方程组,求出坐标.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各点,并将各组内的这些点依次用线段连接起来.

①![]() ,
,![]() ,
,![]() ;②
;②![]() ,
,![]() ,
,![]() ,
,![]() .
.
观察所描出的图形,解答下列问题:
(1)坐标轴上的点有_________,![]() 轴上的点_______坐标等于零,
轴上的点_______坐标等于零,![]() 轴上的点_____坐标等于零.
轴上的点_____坐标等于零.
(2)线段![]() 与
与![]() 轴_______,点
轴_______,点![]() 和点
和点![]() _______坐标相同,线段
_______坐标相同,线段![]() 上其他点_____坐标相同.
上其他点_____坐标相同.
(3)线段![]() 与
与![]() 轴_______,点
轴_______,点![]() 和点
和点![]() _______坐标相同,线段
_______坐标相同,线段![]() 上其他点_____坐标相同.
上其他点_____坐标相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,边
中,边![]() 在
在![]() 轴上,点
轴上,点![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且交边
且交边![]() 于
于![]() ,另有一条直线
,另有一条直线![]() 与
与![]() 平行且分别交
平行且分别交![]() ,
,![]() 于
于![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的长;
的长;
(2)当![]() 为菱形时,求直线
为菱形时,求直线![]() 解析式;
解析式;
(3)当直线![]() 将矩形
将矩形![]() 分成两个面积比例为
分成两个面积比例为![]() 的梯形时,直接写出此时直线
的梯形时,直接写出此时直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,2011年春季以来,我省遭受了严重的旱情,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.
请根据信息解答下列问题:
(1)图1中淘米水浇花所占的百分比为 ;
(2)图1中安装节水设备所在的扇形的圆心角度数为 ;
(3)补全图2;
(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象与
的图象与 ![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与 ![]() 轴交于点C,顶点为D.
轴交于点C,顶点为D.
(1)求点A、B的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)设一次函数 ![]() 的图象经过B、D两点,请直接写出满足
的图象经过B、D两点,请直接写出满足 ![]() 的
的 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高农民收入,某区一水果公园引进一种新型蟠桃,蟠桃进价为每公斤40元.上市后通过一段时间的试营销发现:当蟠桃销售单价在每公斤40元至90元之间(含40元和90元)时,每月的销售量![]() (公斤)与销售单价
(公斤)与销售单价![]() (元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(1)求![]() 与
与![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2)如果想要每月获得2400元的利润,那么销售单价应定为每公斤多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 ![]() 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于
的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com