
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
【答案】A
【解析】解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,
∴EH=AEsin∠EAH≈1.2×0.60=0.72(米),
∵AB=1.2米,
∴AB+EH≈1.2+0.72=1.92≈1.9米.
故选:A.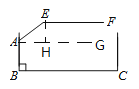
过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AEsin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
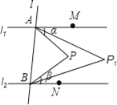
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ![]() ,则MN的长为。
,则MN的长为。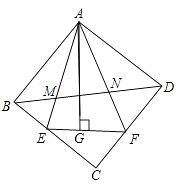
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
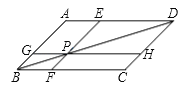
A. 1对B. 2对C. 3对D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据: ![]() ≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( ) 
A.7.27
B.16.70
C.17.70
D.18.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从![]() 地出发前往
地出发前往![]() 地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达
地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达![]() 地.下图是甲、乙两车离开
地.下图是甲、乙两车离开![]() 地的路程
地的路程![]() 与时间
与时间![]() 之间的函数图象.
之间的函数图象.

(1)甲车每小时行驶_________千米,![]() 的值为________.
的值为________.
(2)求甲车再次行驶过程中![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)甲、乙两车离开![]() 地的路程差为8千米时,直接写出
地的路程差为8千米时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽想用一块面积为![]() 的正方形纸片,沿着边的方向裁出一块面积为
的正方形纸片,沿着边的方向裁出一块面积为![]() 的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
的长方形纸片,使它的长宽之比为4:3,他不知道能否裁的出来,正在发愁,请你用所学知识帮小丽分析,能否裁出符合要求的纸片.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为矩形
为矩形![]() 的对角线,将边
的对角线,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,将边
处,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处.
处.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 求四边形
求四边形![]() 的面积及
的面积及![]() 与
与![]() 之间的距离.
之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com