Question

【题目】如图，在正方形ABCD中，△AEF的顶点E，F分别在BC、CD边上，高AG与正方形的边长相等，连BD分别交AE、AF于点M、N，若EG=4，GF=6，BM= ，则MN的长为。

Answer 1

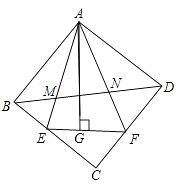
【答案】
【解析】解：如图，连接GM，GN，

∵AG=AB，AE=AE，
∴△AGE≌△ABE，
同理可证△AGF≌△ADF，
∴BE=EG=4，DF=FG=6，
设正方形的边长为a，在Rt△CEF中，CE=a-4，CF=a-6，
由勾股定理，得CE2+CF2=EF2 ， 即（a-4）2+（a-6）2=102 ，
解得a=12或-2（舍去负值），
∴BD=12 ， 易证△ABM≌△AGM，△ADN≌△AGN，
∴MG=BM=3 ，NG=ND=1 -3 -MN=9 -MN， ∠MGN=∠MGA+∠NGA=∠MBA+∠NDA=90°，
在Rt△GMN中，由勾股定理，得MG2+NG2=MN2 ， 即（3 ）2+（9 -MN）2=MN2 ，
解得MN=5
所以答案是：5 ．
【考点精析】通过灵活运用勾股定理的概念，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．