
【题目】如图,直线![]() 上有
上有![]() 、
、![]() 两点,
两点,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,OA=2OB.
上的一点,OA=2OB.
(1)![]() ________
________![]() ,
,![]() ________
________![]() ;
;
(2)若点C是线段AB上一点,且满足![]() ,求CO的长;
,求CO的长;
(3)若动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,在直线
同时出发,在直线![]() 上向右运动.点P的速度为
上向右运动.点P的速度为![]() ,点
,点![]() 的速度为
的速度为![]() ,设动点
,设动点![]() 、
、![]() 运动的时间为
运动的时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 、
、![]() 两点都停止运动,求当
两点都停止运动,求当![]() 为何值时,
为何值时,![]() .
.
![]()
【答案】(1) 8,4;(2) ![]() 的长为
的长为![]() ;(3) 当
;(3) 当![]() 或
或![]() 时,
时,![]() .
.
【解析】
(1)由于AB=12cm,点O是线段AB上的一点,OA=2OB,则OA+OB=3OB=AB=12cm,依此即可求解;
(2)根据图形可知,点C是线段AO上的一点,可设C点所表示的实数为x,分两种情况:①点C在线段OA上时,则x<0,②点C在线段OB上时,则x>0,根据AC=CO+CB,列出方程求解即可;
(3)分0≤t<4;4≤t<6;t≥6三种情况讨论求解即可;
解:(1)![]() AB=12cm, OA=2OB
AB=12cm, OA=2OB
![]() OA+OB=3OB=AB=12cm
OA+OB=3OB=AB=12cm
![]() OA=8,OB=4.
OA=8,OB=4.
(2)设![]() 的长为
的长为![]() ,
,![]() ,
,![]() .
.
答:![]() 的长为
的长为![]() .
.
(3)当0≤t<4时,依题意有:
2(8-2t)-(4+t)=4,
解得t=![]() ;
;
当4≤t<6时,依题意有:
2(2t-8)-(4+t)=4,
解得t=8(不合题意舍去);
当t≥6时,依题意有:
2(2t-8)-(4+t)=4,
解得t=8.
故当t为![]() s或8s时,2OP-OQ=4;
s或8s时,2OP-OQ=4;


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、B(0,﹣3)两点.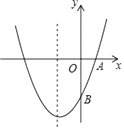
(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(注:方差公式 ![]() .)
.)
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为 ![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
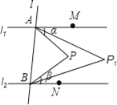
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为 ![]() ,所以
,所以 ![]() ,从而
,从而 ![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:函数 ![]() (常数m>0,x>0),由阅读1结论可知:
(常数m>0,x>0),由阅读1结论可知: ![]()
![]() ,所以当
,所以当 ![]() 即
即 ![]() 时,函数
时,函数 ![]() 的最小值为
的最小值为 ![]() .
.
阅读理解上述内容,解答下列问题:
(1)问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ![]() ,周长为
,周长为 ![]() ,求当x=时,周长的最小值为 .
,求当x=时,周长的最小值为 .
(2)问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, ![]() 的最小值为 .
的最小值为 .
(3)问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
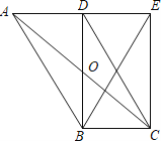
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据: ![]() ≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( ) 
A.7.27
B.16.70
C.17.70
D.18.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com