
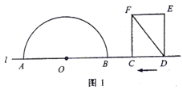
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
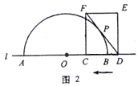
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)如图2,连接OP,则DF与半圆相切,利用△OPD≌△FCD(AAS),可得:OD=DF=30;
(2)利用![]() ,求出
,求出![]() ,则
,则![]() ;DF与半圆相切,由(1)知:PD=CD=18,即可求解;
;DF与半圆相切,由(1)知:PD=CD=18,即可求解;
(3)设PG=GH=m,则:![]()
![]()
![]() ,求出
,求出![]() ,利用
,利用![]() ,即可求解.
,即可求解.
(1)如图,连接![]()

∵![]() 与半圆相切,∴
与半圆相切,∴![]() ,∴
,∴![]() ,
,
在矩形![]() 中,
中,![]() ,
,
∵![]() ,根据勾股定理,得
,根据勾股定理,得
![]()
在![]() 和
和![]() 中,
中,
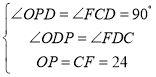
∴![]()
∴![]()
(2)如图,
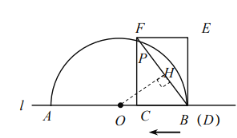
当点![]() 与点
与点![]() 重合时,
重合时,
过点![]() 作
作![]() 与点
与点![]() ,则
,则![]()
∵![]()
且![]() ,由(1)知:
,由(1)知:![]()
∴![]() ,∴
,∴![]() ,
,
∴![]()
当![]() 与半圆相切时,由(1)知:
与半圆相切时,由(1)知:![]() ,
,
∴![]()
(3)设半圆与矩形对角线交于点P、H,过点O作OG⊥DF,
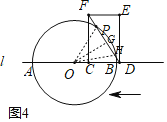
则PG=GH,
![]() ,则
,则![]() ,
,
设:PG=GH=m,则:![]() ,
,
![]() ,
,
整理得:25m2-640m+1216=0,
解得:![]() ,
,
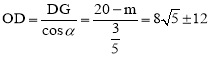 .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与y轴交于点C,连接AC,BC,将
,与y轴交于点C,连接AC,BC,将![]() 沿BC所在的直线翻折,得到
沿BC所在的直线翻折,得到![]() ,连接OD.
,连接OD.
(1)用含a的代数式表示点C的坐标.
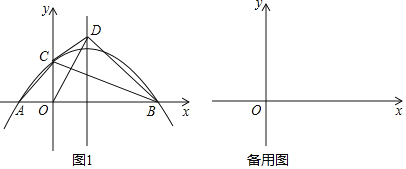
(2)如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,若
的面积为S2,若![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队独自完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度![]() (米)与维修时间
(米)与维修时间![]() (时)之间的函数图象如图所示,下列说法中:
(时)之间的函数图象如图所示,下列说法中:
(1)甲队调离时,甲、乙两队已维修路面的总长度为150米;
(2)乙队每小时比甲队多维修20米;
(3)乙一共工作2小时;
(4)![]() .
.
正确的有( )个.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
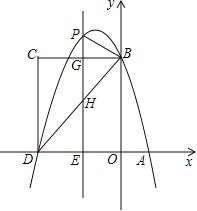
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
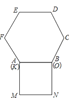
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店3月份购进甲种水果50千克、乙种水果80千克,共花费1700元,其中甲种水果以15元/千克,乙种水果以20元/千克全部售出;4月份又以同样的价格购进甲种水果60千克、乙种水果40千克,共花费1200元,由于市场不景气,4月份两种水果均以3月份售价的8折全部售出.
(1)求甲、乙两种水果的进价每千克分别是多少元?
(2)请计算该水果店3月和4月甲、乙两种水果总赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华人民共和国《城市道路路内停车泊位设置规范》规定:
一、在城市道路范围内,在不影响行人、车辆通行的情况下,政府有关部门可以规划停车泊位.停车泊位的排列方式有三种,如图所示:
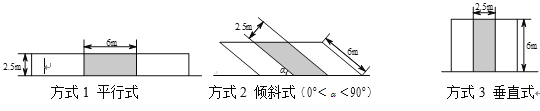
二、双向通行道路,路幅宽![]() 米以上的,可在两侧设停车泊位,路幅宽
米以上的,可在两侧设停车泊位,路幅宽![]() 米到
米到![]() 米的,可在单侧设停车泊位,路幅宽
米的,可在单侧设停车泊位,路幅宽![]() 米以下的,不能设停车泊位;
米以下的,不能设停车泊位;
三、规定小型停车泊位,车位长![]() 米,车位宽
米,车位宽![]() 米;
米;
四、设置城市道路路内机动车停车泊位后,用于单向通行的道路宽度应不小于![]() 米.
米.
根据上述的规定,在不考虑车位间隔线和车道间隔线的宽度的情况下,如果在一条路幅宽为![]() 米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
(1)可在该道路两侧设置停车泊位的排列方式为 ;
(2)如果这段道路长![]() 米,那么在道路两侧最多可以设置停车泊位 个.
米,那么在道路两侧最多可以设置停车泊位 个.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的解析式为
的解析式为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.![]() 确定抛物线的开口方向与大小
确定抛物线的开口方向与大小
B.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() ,
,![]() 的值不变
的值不变
C.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() 的值不变
的值不变
D.若将抛物线![]() 沿直线
沿直线![]() :
:![]() 平移,则
平移,则![]() 、
、![]() 、
、![]() 的值全变
的值全变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com