
【题目】在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与y轴交于点C,连接AC,BC,将
,与y轴交于点C,连接AC,BC,将![]() 沿BC所在的直线翻折,得到
沿BC所在的直线翻折,得到![]() ,连接OD.
,连接OD.
(1)用含a的代数式表示点C的坐标.
(2)如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,若
的面积为S2,若![]() ,求a的值.
,求a的值.
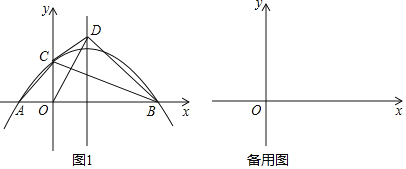
【答案】(1)![]() ;
;
(2) 抛物线的表达式为:![]() ;
;
(3) ![]() 或
或![]()
【解析】
(1)根据待定系数法,得到抛物线的表达式为:![]() ,即可求解;
,即可求解;
(2)根据相似三角形的判定证明![]() ,再根据相似三角形的性质得到
,再根据相似三角形的性质得到![]() ,即可求解;
,即可求解;
(3)连接OD交BC于点H,过点H、D分别作x轴的垂线交于点N、M,由三角形的面积公式得到![]() ,
,![]() ,
,![]() ,而
,而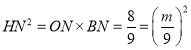 ,即可求解.
,即可求解.
(1)抛物线的表达式为:![]() ,即
,即![]() ,则点
,则点![]() ;
;
(2)过点B作y轴的平行线BQ,过点D作x轴的平行线交y轴于点P、交BQ于点Q,
∵![]() ,
,![]() ,
,
∴![]() ,
,
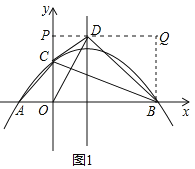
设:![]() ,点
,点![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
其中:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
将以上数值代入比例式并解得:![]() ,
,
∵![]() ,故
,故![]() ,
,
故抛物线的表达式为:![]() ;
;
(3)如图2,当点C在x轴上方时,连接OD交BC于点H,则![]() ,
,
过点H、D分别作x轴的垂线交于点N、M,
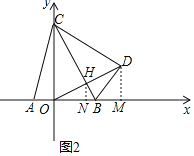
设:![]() ,
,
![]() ,
,
![]() ,而
,而![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,则
,则![]() ,
,
则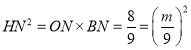 ,
,
解得:![]() (舍去负值),
(舍去负值),
![]() ,
,
解得:![]() (不合题意值已舍去),
(不合题意值已舍去),
故:![]() .当点C在x轴下方时,同理可得:
.当点C在x轴下方时,同理可得:![]() ;故:
;故:![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC上一点(能与B重合,不与C重合),以DC为直径的半圆O,交AC于点E.
(1)如图1,若点D与点B重合,半圆交AB于点F,求证:AE=AF.
(2)设∠B=60°,若半圆与AB相切于点T,在图2中画出相应的图形,求∠AET的度数.
(3)设∠B=60°,BC=6,△ABC的外心为点P,若点P正好落在半圆与其直径组成的封闭图形的内部,直接写出DC的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
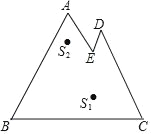
【题目】对于封闭的平面图形,如果图形上或图形内的点S到图形上的任意一点P之间的线段都在图形内或图形上,那么这样的点S称为“亮点”.如图,对于封闭图形ABCDE,S1是“亮点”,S2不是“亮点”,如果AB∥DE,AE∥DC,AB=2,AE=1,∠B=∠C=60°,那么该图形中所有“亮点”组成的图形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,商丘市正在围绕打响“游商丘古都城,读华夏文明史”文化旅游品牌,加快推进商丘景点保护性修复与宣传工作,以此带动以文化为核心的全域旅游跨越发展,打造华夏历史文明商丘传承创新区.随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,某中学开展以“我最喜欢的商丘风景区”为主题的调查活动,围绕“在森林公园、日月湖、汉梁公园和睢阳古城”四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
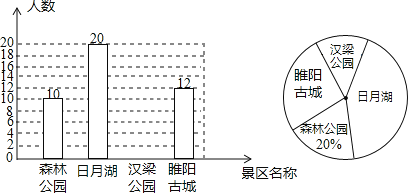
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该中学共有3000名学生,请你估计最喜欢日月湖风景区的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
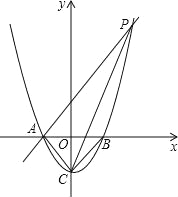
(1)求A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日是新中国成立70周年.某学校国庆节后,为了调查学生对这场阅兵仪式的关注情况,在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试,批改试卷后,学校政教处随机抽取了部分学生的考卷进行成绩统计,发现成绩最低是51分,最高是100分,根据统计结果,绘制了如下尚不完整的统计图表.
调查结果频数分布表
分数段/分 | 频数 | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
| 0.25 |
| 35 |
|
| 12 | 0.12 |
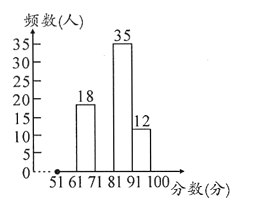
请根据以上信息,解答下列问题:
(1)![]() ;
;
(2)若把上面频数分布表中的信息画在扇形统计图内,则![]() 所在扇形圆心角的度数是 ;
所在扇形圆心角的度数是 ;
(3)请将频数分布直方图补充完整;
(4)若该校有1200名学生,请估计该校分数![]() 在
在![]() 范围的学生有多少名.
范围的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
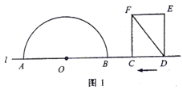
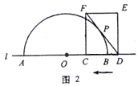
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com